题目内容
如图,设△OEP的面积为S,已知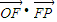 =1.
=1.(1)若
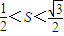 ,求向量
,求向量 与
与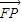 的夹角θ的取值范围;
的夹角θ的取值范围;(2)若S=
 |
|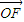 |,且|
|,且|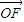 |≥2,当|
|≥2,当|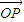 |取最小值时,建立适当的直角坐标系,求以O为中心,F为一个焦点且经过点P的椭圆方程.
|取最小值时,建立适当的直角坐标系,求以O为中心,F为一个焦点且经过点P的椭圆方程.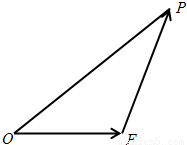
【答案】分析:(Ⅰ)令  ,由题设知
,由题设知  ,
, ,∵
,∵ ,∴
,∴ ,由此可求出
,由此可求出  的范围..
的范围..
(Ⅱ)以O为原点,OF所在直线为x轴建立直角坐标系,并令Q(m,n),则F(c,0),由题设知 .
. ,
, .由此知
.由此知  ,由此入手,当
,由此入手,当  取最小值时,能够求出椭圆的方程.
取最小值时,能够求出椭圆的方程.
解答:解:(Ⅰ)令 ,
,
∵ ,∴
,∴ ,∴
,∴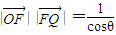 ,
,
∵ =
= ,
,
∴ ,∵
,∵ ,∴
,∴ ,
,
∵θ∈[0,π],∴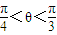 .
.
(Ⅱ)以O为原点,OF所在直线为x轴建立直角坐标系,并令Q(m,n),则F(c,0),
且 ,∴
,∴ .
.
∵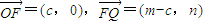 ,
,
∴ .
.
∴ ,∴
,∴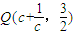 .
.
∴ ,
,
∵c≥2,
∴当c=2时, 最小,此时Q(
最小,此时Q(  ),
),
设椭圆方程为 ,
,
∴ ,
,
∴a2=10,b2=6.
∴所求椭圆为 .
.
点评:本题考查圆锥曲线的性质和应用,解题时要认真审题,仔细解答,注意积累解题方法.
 ,由题设知
,由题设知  ,
, ,∵
,∵ ,∴
,∴ ,由此可求出
,由此可求出  的范围..
的范围..(Ⅱ)以O为原点,OF所在直线为x轴建立直角坐标系,并令Q(m,n),则F(c,0),由题设知
 .
. ,
, .由此知
.由此知  ,由此入手,当
,由此入手,当  取最小值时,能够求出椭圆的方程.
取最小值时,能够求出椭圆的方程.解答:解:(Ⅰ)令
 ,
,∵
 ,∴
,∴ ,∴
,∴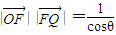 ,
,∵
 =
= ,
,∴
 ,∵
,∵ ,∴
,∴ ,
,∵θ∈[0,π],∴
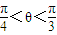 .
.(Ⅱ)以O为原点,OF所在直线为x轴建立直角坐标系,并令Q(m,n),则F(c,0),
且
 ,∴
,∴ .
.∵
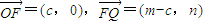 ,
,∴
 .
.∴
 ,∴
,∴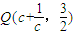 .
.∴
 ,
,∵c≥2,
∴当c=2时,
 最小,此时Q(
最小,此时Q(  ),
),设椭圆方程为
 ,
,∴
 ,
,∴a2=10,b2=6.
∴所求椭圆为
 .
.点评:本题考查圆锥曲线的性质和应用,解题时要认真审题,仔细解答,注意积累解题方法.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
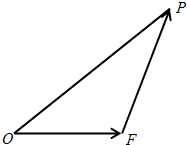 如图,设△OEP的面积为S,已知
如图,设△OEP的面积为S,已知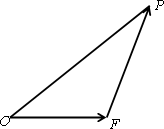
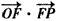 =1,
=1, ,求向量
,求向量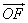 与
与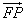 的夹角θ的取值范围;
的夹角θ的取值范围;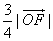 且
且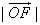 ≥2,当
≥2,当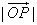 取最小值时,建立适当的直角坐标系,求以O为中心,F为一个焦点且经过点P的椭圆方程。
取最小值时,建立适当的直角坐标系,求以O为中心,F为一个焦点且经过点P的椭圆方程。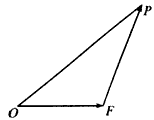
 =1.
=1. ,求向量
,求向量 与
与 的夹角θ的取值范围;
的夹角θ的取值范围; |
| |,且|
|,且| |≥2,当|
|≥2,当| |取最小值时,建立适当的直角坐标系,求以O为中心,F为一个焦点且经过点P的椭圆方程.
|取最小值时,建立适当的直角坐标系,求以O为中心,F为一个焦点且经过点P的椭圆方程.