题目内容
已知复数Z=2m-1+(m+1)i(1)若复数Z所对应的点在第一象限,求实数m的取值范围;
(2)若复数
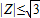 ,求实数m的取值范围.
,求实数m的取值范围.
【答案】分析:(1)写出复数z的共轭复数,对应的点在第一象限,说明其实部大于0,虚部大于0,列不等式求解a的取值范围.
(2)利用复数的模的关系式,直接列出不等式求解即可.
解答:解:(1)复数Z=2m-1+(m+1)i
若复数Z所对应的点在第一象限,
则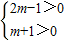 ,解得:m>
,解得:m> ,
,
所以数对应的点在第一象限的实数m的取值范围是{m|m> }.
}.
(2)因为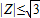 ,所以
,所以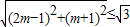 ,解得
,解得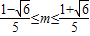 .
.
点评:本题考查了复数的基本概念,关键是读懂题意,把问题转化为方程或不等式组求解,此题是基础题.
(2)利用复数的模的关系式,直接列出不等式求解即可.
解答:解:(1)复数Z=2m-1+(m+1)i
若复数Z所对应的点在第一象限,
则
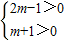 ,解得:m>
,解得:m> ,
,所以数对应的点在第一象限的实数m的取值范围是{m|m>
 }.
}.(2)因为
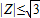 ,所以
,所以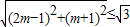 ,解得
,解得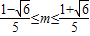 .
.点评:本题考查了复数的基本概念,关键是读懂题意,把问题转化为方程或不等式组求解,此题是基础题.

练习册系列答案
相关题目