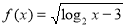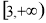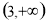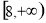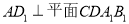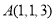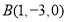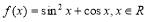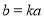题目内容
如图,四棱锥 中,
中, ∥
∥ ,
, ,侧面
,侧面 为等边三角形
为等边三角形

(1)证明:
(2)求AB与平面SBC所成角的正弦值
(1)参考解析;(2)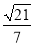
【解析】
试题分析:(1)要证 ,从原图中较难找出线与线的垂直,通过取线段AB的中点E,并连接DE,可求出SE,DE的长结合已知SD的长,可得
,从原图中较难找出线与线的垂直,通过取线段AB的中点E,并连接DE,可求出SE,DE的长结合已知SD的长,可得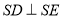 再通过证明
再通过证明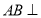 平面
平面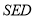 可得
可得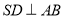 从而可得
从而可得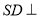 平面
平面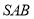
(2)求AB与平面SBC所成角的正弦值,因为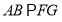 ,所以所求的问题等价于
,所以所求的问题等价于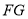 与平面SBC所成角的正弦值 只需要证明平面
与平面SBC所成角的正弦值 只需要证明平面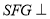 平面,从而作出
平面,从而作出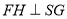 即可得
即可得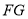 与平面SBC所成角为
与平面SBC所成角为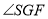 通过解三角形即可得结论
通过解三角形即可得结论
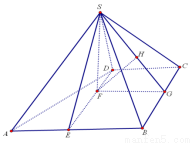
试题解析:(1)证明:取AB中点E,连结DE,则四边形BCDE为矩形,DE=CB=2。
连结SE,则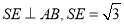
又SD=1,故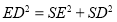
所以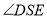 为直角。
为直角。
由 ,得
,得
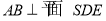 ,所以
,所以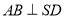
SD与两条相交直线AB、SE都垂直。
所以 6分
6分
(II)由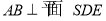 知,
知,
作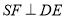 ,垂足为F,
,垂足为F,
则 ,
,
作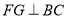 ,垂足为G,则FG=DC=1。
,垂足为G,则FG=DC=1。
连结SG,则
又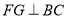 ,
,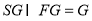 ,
,
故 ,
,
作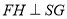 ,H为垂足,则
,H为垂足,则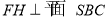
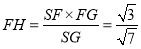
即F到平面SBC的距离为
由于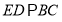 ,所以
,所以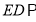 平面
平面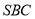 ,E到平面
,E到平面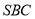 的距离d也为
的距离d也为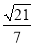 设AB与平面
设AB与平面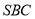 所成的角为
所成的角为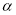 ,则
,则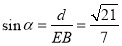
考点:1 线面垂直的知识 2 面面垂直的知识 3 直线与平面所成角的概念 4 线面转化的思想 5 提升探索,分类的能力

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目