题目内容
已知△ABC的面积是30,其内角A、B、C所对边的长分别为a,b,c,且满足cosA=| 12 | 13 |
分析:由cosA=
可得sinA=
,结合结合三角形的面积可求bc,而已知c-b=1,且cosA=
,要求a,考虑利用余弦定理a2=b2+c2-2bccosA,从而可求答案.
| 12 |
| 13 |
| 5 |
| 13 |
| 12 |
| 13 |
解答:解:∵cosA=
∴sinA=
∵S△ABC=
bcsinA=30∴bc=156
由余弦定理可得,a2=b2+c2-2bccosA
=(c-b)2+2bc-2bc×
=25
∴a=5
故答案为:5
| 12 |
| 13 |
| 5 |
| 13 |
∵S△ABC=
| 1 |
| 2 |
由余弦定理可得,a2=b2+c2-2bccosA
=(c-b)2+2bc-2bc×
| 12 |
| 13 |
∴a=5
故答案为:5
点评:本题主要考查的正弦定理、余弦定理及三角形的面积公式等知识的综合运用,在解三角形的问题中若把三角形的面积与余弦定理结合时常用整体思想求解出两边的积及和(或差),而不要直接解出边.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
已知△ABC的面积是30,内角A、B、C所对边分别为a、b、c,cosA=
.若c-b=1,则a的值是( )
| 12 |
| 13 |
| A、3 | B、4 | C、5 | D、不确定 |
 ,已知△ABC的面积是1,则△PAB的面积是
。
,已知△ABC的面积是1,则△PAB的面积是
。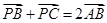 ,已知△ABC的面积是1,则△PAB的面积是
。
,已知△ABC的面积是1,则△PAB的面积是
。