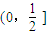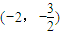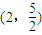题目内容
设a,b∈R且a≠2,函数f(x)=lg
在区间(-b,b)上是奇函数.
(Ⅰ)求ab的取值集合;
(Ⅱ)讨论函数f(x)在 (-b,b)上的单调性.
| 1+ax |
| 1+2x |
(Ⅰ)求ab的取值集合;
(Ⅱ)讨论函数f(x)在 (-b,b)上的单调性.
(I)函数f(x)=lg
在区间(-b,b)内是奇函数
∴对任意x∈(-b,b)都有f(-x)+f(x)=0,
∴lg
+lg
=lg
=0
即
=1
即a2x2=4x2,此式对任意x∈(-b,b)都成立
∴a2=4
又∵a≠2,∴a=-2
代入
,得
>0,即-
<x<
此式对任意x∈(-b,b)都成立,相当于-
<-b<b<
所以b的取值范围是(0,
]
∴ab的取值集合为[-1,0)
(II)设任意的x1,x2∈(-b,b),且x1<x2,由b∈(0,
]得
所以0<1-2x2<1-2x1,0<1+2x1<1+2x2
从而f(x2)-f(x1)=lg
-lg
=lg
<lg1=0
∴f(x2)<f(x1)
因此f(x)在(-b,b)内是减函数?
| 1+ax |
| 1+2x |
∴对任意x∈(-b,b)都有f(-x)+f(x)=0,
∴lg
| 1-ax |
| 1-2x |
| 1+ax |
| 1+2x |
| 1-a2x2 |
| 1-4x2 |
即
| 1-a2x2 |
| 1-4x2 |
即a2x2=4x2,此式对任意x∈(-b,b)都成立
∴a2=4
又∵a≠2,∴a=-2
代入
| 1+ax |
| 1+2x |
| 1-2x |
| 1+2x |
| 1 |
| 2 |
| 1 |
| 2 |
此式对任意x∈(-b,b)都成立,相当于-
| 1 |
| 2 |
| 1 |
| 2 |
所以b的取值范围是(0,
| 1 |
| 2 |
∴ab的取值集合为[-1,0)
(II)设任意的x1,x2∈(-b,b),且x1<x2,由b∈(0,
| 1 |
| 2 |
所以0<1-2x2<1-2x1,0<1+2x1<1+2x2
从而f(x2)-f(x1)=lg
| 1-2x2 |
| 1+2x2 |
| 1-2x1 |
| 1+2x1 |
| (1-2x2)(1+2x1) |
| (1+2x2)(1-2x1) |
∴f(x2)<f(x1)
因此f(x)在(-b,b)内是减函数?

练习册系列答案
相关题目
设a,b∈R且a≠2若定义在区间(-b,b)上的函数f(x)=lg
是奇函数.则a+b的取值范围是( )
| 1+ax |
| 1+2x |
A、(0,
| ||
B、(-2,-
| ||
C、(2,
| ||
D、(-2,-
|
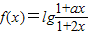 在区间(-b,b)上是奇函数.
在区间(-b,b)上是奇函数.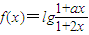 是奇函数.则a+b的取值范围是( )
是奇函数.则a+b的取值范围是( )