Question

设S₁=1²，S₂=1²+2²+1²，S₃=1²+2²+3²+2²+1²，…，
S_n=1²+2²+3²+…+n²+…+3²+2²+1²，…
用数学归纳法证明：公式Sn=

n(2n2+1)

3

对所有的正整数n都成立．

Answer 1

分析：本题考查的知识点是数学归纳法，由数学归纳法的步骤，我们先判断n=1时Sn=

n(2n2+1)

3

对是否成立，然后假设当n=k时，公式Sn=

n(2n2+1)

3

成立，只要能证明出当n=k+1时，公式Sn=

n(2n2+1)

3

成立即可得到公式Sn=

n(2n2+1)

3

对所有的正整数n都成立．

解答：证明：因为S_n=1²+2²+3²+…+n²+…+3²+2²+1²，即要证明
1²+2²+3²+…+n²+…+3²+2²+1²=

n(2n2+1)

3

，（A）
（Ⅰ）当n=1，左边=1，右=

1•3

3

=1，故（A）式成立
（Ⅱ）假设当n=k时，（A）式成立，即
1²+2²+3²+…+k²+…+3²+2²+1²=

k(2k2+1)

3

现设n=k+1，在上式两边都加上（k+1）²+k²，得
1²+2²+3²+…+k²+（k+1）²+k²+…+3²+2²+1²=

k(2k2+1)

3

+（k+1）²+k²，
=

2k3+k+3(k+1)2+3k2

3

=

k(2k+1)(k+1)+3(k+1)2

3

=

(k+1)(2k2+4k+3)

3

=

(k+1)[2(k+1)2+1]

3

．
即证得当n=k+1时（A）式也成立根据（Ⅰ）和（Ⅱ），
（A）式对所有的正整数n都成立，即证得Sn=

n(2n2+1)

3

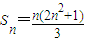点评：数学归纳法的步骤：①证明n=1时A式成立②然后假设当n=k时，A式成立③证明当n=k+1时，A式也成立④下绪论：A式对所有的正整数n都成立．