题目内容
设S1=12,S2=12+22+12,S3=12+22+32+22+12,…,Sn=12+22+…+n2+…+22+12,…,某学生猜测Sn=n(an2+b),老师:回答正确,则a+b=分析:根据已知中S1=12,S2=12+22+12,S3=12+22+32+22+12,…,我们归纳分析后,即可得到一个关于Sn的表达式,进而确定出a,b的值后,即可得到答案.
解答:解:∵S1=12=1×(
×12+
),
S2=12+22+12=2×(
×22+
),
S3=12+22+32+22+12=3×(
×32+
),
…,
由此我们可以推断
Sn=12+22+…+n2+…+22+12=n×(
×n2+
),
故a=
,b=
,
∴a+b=1
故答案为:1
| 2 |
| 3 |
| 1 |
| 3 |
S2=12+22+12=2×(
| 2 |
| 3 |
| 1 |
| 3 |
S3=12+22+32+22+12=3×(
| 2 |
| 3 |
| 1 |
| 3 |
…,
由此我们可以推断
Sn=12+22+…+n2+…+22+12=n×(
| 2 |
| 3 |
| 1 |
| 3 |
故a=
| 2 |
| 3 |
| 1 |
| 3 |
∴a+b=1
故答案为:1
点评:本题考查的知识点是归纲推理,其中根据已知中S1=12,S2=12+22+12,S3=12+22+32+22+12,…及某学生猜测Sn=n(an2+b),老师回答正确,而将问题转化为一个方程问题是解答的关键.

练习册系列答案
相关题目
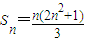 对所有的正整数n都成立.
对所有的正整数n都成立.