题目内容
已知两个向量集合:P=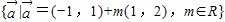 ,Q=
,Q=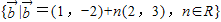 ,则P∩Q=( )
,则P∩Q=( )A.{(1,-2)}
B.{(-13,-23)}
C.{(-2,1)}
D.{(-23,-13)}
【答案】分析:根据数乘向量及向量加法的坐标运算,我们可以化简集合P,Q中元素的性质,进而计算出两个集合求交时,参数m,n的值,进而得到P∩Q的值.
解答:解:∵向量集合:P=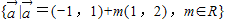 =
= ,
,
向量集合:Q= =
=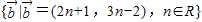 ,
,
令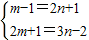
解得:m=-12,n=-7
故P∩Q={(-13,-23)}
故选B
点评:本题考查的知识点是平面向量的表示的应用,相等向量与相反向量,其中根据两个向量相等,其中横纵坐标均相等构造关于m,n的方程,是解答本题的关键.
解答:解:∵向量集合:P=
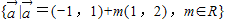 =
= ,
,向量集合:Q=
 =
=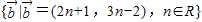 ,
,令
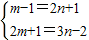
解得:m=-12,n=-7
故P∩Q={(-13,-23)}
故选B
点评:本题考查的知识点是平面向量的表示的应用,相等向量与相反向量,其中根据两个向量相等,其中横纵坐标均相等构造关于m,n的方程,是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
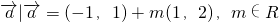 ,Q=
,Q=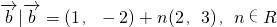 ,则P∩Q=
,则P∩Q=