题目内容
△ABC是以A为钝角的三角形,且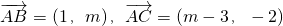 ,则m的取值范围是________.
,则m的取值范围是________.
(-3,1)∪(1,2)∪(2,+∞)
分析:根据角A是钝角,可得数量积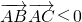 ,结合坐标运算解得m>-3;又因为向量
,结合坐标运算解得m>-3;又因为向量 是不共线的向量,可得1×(-2)≠(m-3)m,解之得m≠1且m≠2.两者相结合即可得到本题的答案.
是不共线的向量,可得1×(-2)≠(m-3)m,解之得m≠1且m≠2.两者相结合即可得到本题的答案.
解答:∵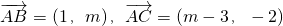 ,且A为钝角
,且A为钝角
∴ =1×(m-3)+m×(-2)<0,解之得m>-3
=1×(m-3)+m×(-2)<0,解之得m>-3
又∵A、B、C三点不共线,得向量 是不共线的向量
是不共线的向量
∴1×(-2)≠(m-3)m,即m2-3m+2≠0,解之得m≠1且m≠2
因此,实数m的取值范围是(-3,1)∪(1,2)∪(2,+∞)
故答案为(-3,1)∪(1,2)∪(2,+∞)
点评:本题给出向量 的坐标含有参数m,在它们夹钝角的情况下求参数m的取值范围.着重考查了向量平行的条件、向量数量积的坐标运算公式等知识,属于基础题.
的坐标含有参数m,在它们夹钝角的情况下求参数m的取值范围.着重考查了向量平行的条件、向量数量积的坐标运算公式等知识,属于基础题.
分析:根据角A是钝角,可得数量积
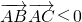 ,结合坐标运算解得m>-3;又因为向量
,结合坐标运算解得m>-3;又因为向量 是不共线的向量,可得1×(-2)≠(m-3)m,解之得m≠1且m≠2.两者相结合即可得到本题的答案.
是不共线的向量,可得1×(-2)≠(m-3)m,解之得m≠1且m≠2.两者相结合即可得到本题的答案.解答:∵
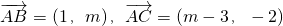 ,且A为钝角
,且A为钝角∴
 =1×(m-3)+m×(-2)<0,解之得m>-3
=1×(m-3)+m×(-2)<0,解之得m>-3又∵A、B、C三点不共线,得向量
 是不共线的向量
是不共线的向量∴1×(-2)≠(m-3)m,即m2-3m+2≠0,解之得m≠1且m≠2
因此,实数m的取值范围是(-3,1)∪(1,2)∪(2,+∞)
故答案为(-3,1)∪(1,2)∪(2,+∞)
点评:本题给出向量
 的坐标含有参数m,在它们夹钝角的情况下求参数m的取值范围.着重考查了向量平行的条件、向量数量积的坐标运算公式等知识,属于基础题.
的坐标含有参数m,在它们夹钝角的情况下求参数m的取值范围.着重考查了向量平行的条件、向量数量积的坐标运算公式等知识,属于基础题. 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
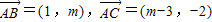 ,则m的取值范围是 .
,则m的取值范围是 .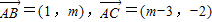 ,则m的取值范围是 .
,则m的取值范围是 .