题目内容
设A,B分别为椭圆 (a>0,b>0)的左、右顶点,椭圆长半轴的长等于焦距,且x=4为它的右准线.
(a>0,b>0)的左、右顶点,椭圆长半轴的长等于焦距,且x=4为它的右准线.
(1)求椭圆的方程;
(2)设点P为椭圆上不同于A,B的一个动点,直线PA,PB与椭圆右准线相交于M,N两点,在x轴上是否存在点Q,使得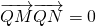 ,若存在,求出点Q的坐标,若不存在,说明理由.
,若存在,求出点Q的坐标,若不存在,说明理由.
解:(1)由题意,知a=2c,=4,解得a=2,c=1,∴b=,故椭圆方程为 …(5分)
…(5分)
(2)设P(2cosθ,sinθ),M(4,m),N(4,n),则A(-2,0),B(2,0),
由A、P、M三点共线,得m=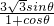 …(7分)
…(7分)
由B、P、N三点共线,得n=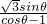 ,…(9分)
,…(9分)
设Q(t,0),则由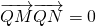 得
得
(t-4)(t-4)+(0-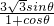 )(0-
)(0-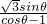 )=0,
)=0,
整理得:(t-4)2-9=0 解得t=1或t=7
∴Q点的坐标是(7,0)或(1,0).…(12分)
分析:(1)由题意,知a=2c, =4,求出a,b 即得出椭圆的方程
=4,求出a,b 即得出椭圆的方程
(2)设P(2cosθ,sinθ),M(4,m),N(4,n),设Q(t,0)利用向量坐标表示及数量积运算,由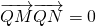 ,列出关于t的方程,判断出解得情况,解得答案.
,列出关于t的方程,判断出解得情况,解得答案.
点评:本题考椭圆的方程求解,向量的运算,及探索性问题,用到了方程思想.
 …(5分)
…(5分)(2)设P(2cosθ,sinθ),M(4,m),N(4,n),则A(-2,0),B(2,0),
由A、P、M三点共线,得m=
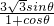 …(7分)
…(7分)由B、P、N三点共线,得n=
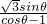 ,…(9分)
,…(9分)设Q(t,0),则由
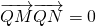 得
得(t-4)(t-4)+(0-
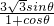 )(0-
)(0-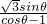 )=0,
)=0,整理得:(t-4)2-9=0 解得t=1或t=7
∴Q点的坐标是(7,0)或(1,0).…(12分)
分析:(1)由题意,知a=2c,
 =4,求出a,b 即得出椭圆的方程
=4,求出a,b 即得出椭圆的方程(2)设P(2cosθ,sinθ),M(4,m),N(4,n),设Q(t,0)利用向量坐标表示及数量积运算,由
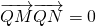 ,列出关于t的方程,判断出解得情况,解得答案.
,列出关于t的方程,判断出解得情况,解得答案.点评:本题考椭圆的方程求解,向量的运算,及探索性问题,用到了方程思想.

练习册系列答案
相关题目