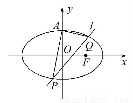
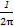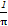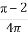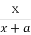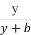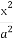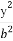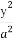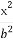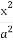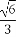题目内容
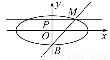
在平面直角坐标系xOy中,已知椭圆C1: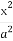 +
+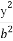 =1(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上,
=1(a>b>0)的左焦点为F1(-1,0),且点P(0,1)在C1上,
(1)求椭圆C1的方程.
(2)设直线l同时与椭圆C1和抛物线C2:y2=4x相切,求直线l的方程.
(1)  +y2=1 (2) y=
+y2=1 (2) y= x+
x+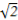 ,y=-
,y=- x-
x-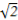
【解析】(1)由题意得c=1,b=1,a=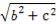 =
=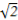 ,
,
∴椭圆C1的方程为 +y2=1.
+y2=1.
(2)由题意得直线的斜率一定存在且不为0,设直线l的方程为y=kx+m.
因为椭圆C1的方程为 +y2=1,
+y2=1,
∴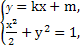
消去y得(1+2k2)x2+4kmx+2m2-2=0.
直线l与椭圆C1相切,
∴Δ=16k2m2-4(2k2+1)(2m2-2)=0.
即2k2-m2+1=0. ①
直线l与抛物线C2:y2=4x相切,则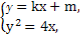
消去y得k2x2+(2km-4)x+m2=0.
∴Δ=(2km-4)2-4k2m2=0,即km=1. ②
由①②解得k= ,m=
,m=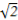 ;k=-
;k=- ,m=-
,m=-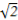 .
.
所以直线l的方程y= x+
x+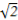 ,y=-
,y=- x-
x-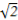 .
.

练习册系列答案
相关题目