题目内容
O为△ABC所在平面上的一点且满足|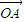 |2+|
|2+|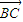 |2=|
|2=| |2+|
|2+|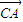 |=|
|=|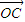 |2+|
|2+|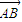 |2,则O为( )
|2,则O为( )A.△ABCK的三条高线的交点
B.△ABCK的三条中线的交点
C.△的三条边的垂直平分线的交点
D.△的三条内角平分线的交点
【答案】分析:根据向量的减法分别用 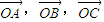 表示
表示 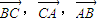 ,利用数量积运算和题意代入式子进行化简,证出OC⊥AB,同理可得OB⊥AC,OA⊥BC,即证出O是△ABC的垂心.
,利用数量积运算和题意代入式子进行化简,证出OC⊥AB,同理可得OB⊥AC,OA⊥BC,即证出O是△ABC的垂心.
解答:解:设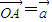 ,
,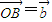 ,
,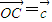 ,则
,则 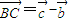 ,
,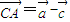 ,
,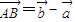 .
.
由题可知,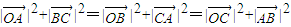 ,
,
∴|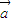 |2+|
|2+| |2=|
|2=|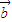 |2+|
|2+|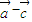 |2,化简可得
|2,化简可得 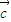 •
•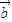 =
=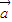 •
•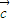 ,即(
,即( 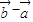 )•
)•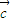 =0,
=0,
∴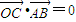 ,∴
,∴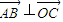 ,即OC⊥AB.
,即OC⊥AB.
同理可得OB⊥AC,OA⊥BC.
∴O是△ABC的垂心.
故选A.
点评:本题考查了向量在几何中应用,主要利用向量的线性运算以及数量积进行化简证明,特别证明垂直主要根据题意构造向量利用数量积为零进行证明.
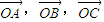 表示
表示 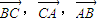 ,利用数量积运算和题意代入式子进行化简,证出OC⊥AB,同理可得OB⊥AC,OA⊥BC,即证出O是△ABC的垂心.
,利用数量积运算和题意代入式子进行化简,证出OC⊥AB,同理可得OB⊥AC,OA⊥BC,即证出O是△ABC的垂心.解答:解:设
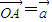 ,
,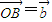 ,
,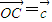 ,则
,则 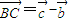 ,
,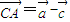 ,
,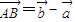 .
.由题可知,
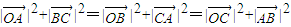 ,
,∴|
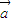 |2+|
|2+| |2=|
|2=|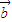 |2+|
|2+|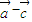 |2,化简可得
|2,化简可得 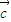 •
•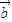 =
=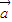 •
•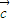 ,即(
,即( 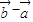 )•
)•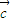 =0,
=0,∴
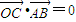 ,∴
,∴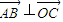 ,即OC⊥AB.
,即OC⊥AB.同理可得OB⊥AC,OA⊥BC.
∴O是△ABC的垂心.
故选A.
点评:本题考查了向量在几何中应用,主要利用向量的线性运算以及数量积进行化简证明,特别证明垂直主要根据题意构造向量利用数量积为零进行证明.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知O为△ABC所在平面内一点,满足|
|2+|
|2=|
|2+|
|2=|
|2+|
|2,则点O是△ABC的( )
| OA |
| BC |
| OB |
| CA |
| OC |
| AB |
| A、外心 | B、内心 | C、垂心 | D、重心 |
O为△ABC所在平面上的一点且满足|
|2+|
|2=|
|2+|
|=|
|2+|
|2,则O为( )
| OA |
| BC |
| OB |
| CA |
| OC |
| AB |
| A、△ABCK的三条高线的交点 |
| B、△ABCK的三条中线的交点 |
| C、△的三条边的垂直平分线的交点 |
| D、△的三条内角平分线的交点 |