题目内容
已知函数f(x)=|log2x|,正实数m,n满足m<n,且f(m)=f(n),若f(x)在区间[m2,n]上的最大值为2,则m,n的值分别为( )
A. ,2 ,2 | B. ,4 ,4 | C. , ,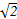 | D. ,4 ,4 |
A
f(x)=|log2x|=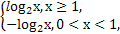
则函数f(x)在(0,1)上是减函数,在(1,+∞)上是增函数,
又m<n且f(m)=f(n),则0<m<1,n>1,
∴0<m2<m<1,
∴f(m2)>f(m)=f(n),
即函数f(x)在区间[m2,n]上的最大值为f(m2).
由题意知f(m2)=2,即-log2m2=2,
∴m= ,由f(m)=f(n)得-log2
,由f(m)=f(n)得-log2 =log2n,∴n=2.
=log2n,∴n=2.
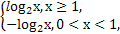
则函数f(x)在(0,1)上是减函数,在(1,+∞)上是增函数,
又m<n且f(m)=f(n),则0<m<1,n>1,
∴0<m2<m<1,
∴f(m2)>f(m)=f(n),
即函数f(x)在区间[m2,n]上的最大值为f(m2).
由题意知f(m2)=2,即-log2m2=2,
∴m=
 ,由f(m)=f(n)得-log2
,由f(m)=f(n)得-log2 =log2n,∴n=2.
=log2n,∴n=2.
练习册系列答案
相关题目
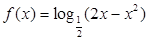 的定义域是_____________.
的定义域是_____________. ,若对于任意
,若对于任意 ,当
,当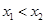 时,总有
时,总有 ,则区间
,则区间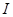 有可能是( )
有可能是( )



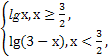 若方程f(x)=k无实数根,则实数k的取值范围是 .
若方程f(x)=k无实数根,则实数k的取值范围是 .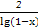 ,则函数f(x)的定义域是( )
,则函数f(x)的定义域是( ) 在函数
在函数 的图象上,则函数
的图象上,则函数 的值域为( )
的值域为( ) 



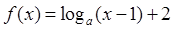 的图象恒过定点( )
的图象恒过定点( ) +lg
+lg  的值是________.
的值是________.