题目内容
设函数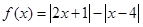 .
.
(I)解不等式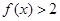 ;
;
(II)求函数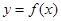 的最小值.
的最小值.
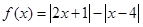 .
.(I)解不等式
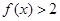 ;
;(II)求函数
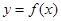 的最小值.
的最小值.(Ⅰ) 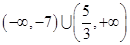 ;(Ⅱ)
;(Ⅱ) 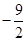 .
.
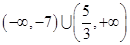 ;(Ⅱ)
;(Ⅱ) 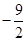 .
.试题分析:(Ⅰ)先将函数
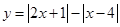 写成分段函数的形式,根据分段函数的解析式作出函数的图像,然后求出直线
写成分段函数的形式,根据分段函数的解析式作出函数的图像,然后求出直线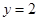 与函数图像的交点坐标为
与函数图像的交点坐标为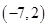 和
和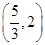 ,利用数形结合的思想可知
,利用数形结合的思想可知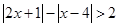 的解集;(Ⅱ)找到函数图像的最低点,求出最低点的纵坐标即可.
的解集;(Ⅱ)找到函数图像的最低点,求出最低点的纵坐标即可.试题解析:(Ⅰ)令
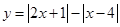 ,则有
,则有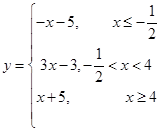 ,
,则作出函数
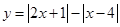 的图像如下:
的图像如下: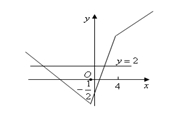
它与直线
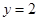 的交点为
的交点为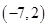 和
和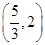 .
.所以
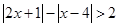 的解集为:
的解集为: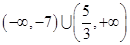 . 6分
. 6分(Ⅱ)由函数
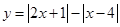 的图像可知,
的图像可知,当
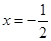 时,函数
时,函数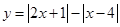 取得最小值
取得最小值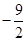 . 10分
. 10分
练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
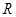 的函数
的函数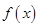 满足
满足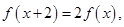 当
当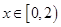 时,
时,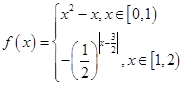 ,若
,若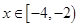 时,
时,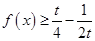 恒成立,则实数
恒成立,则实数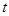 的取值范围是( )
的取值范围是( )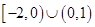
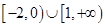

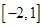
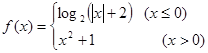 ,若
,若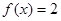 ,则
,则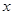 的值是
的值是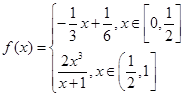 ,函数
,函数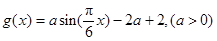 ,若存在
,若存在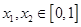 ,使得
,使得 成立,则实数
成立,则实数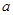 的取值范围是 .
的取值范围是 .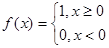 ,则函数
,则函数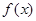 的值域是( ).
的值域是( ). 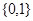
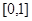
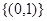
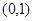
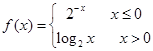 ,则
,则
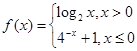 ,则
,则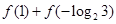 的值为 .
的值为 . ,则
,则 的值是
的值是




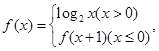 则
则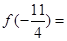 ( )
( )


