题目内容
求函数y=tan2x+tanx+1(x∈R且x≠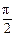 +kπ,k∈Z)的值域.
+kπ,k∈Z)的值域.
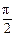 +kπ,k∈Z)的值域.
+kπ,k∈Z)的值域.原函数的值域是[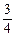 ,+∞)
,+∞)
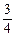 ,+∞)
,+∞) 设t=tanx,由正切函数的值域可得t∈R,
则y=t2+t+1=(t+ )2+
)2+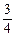 ≥
≥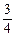 .
.
∴原函数的值域是[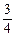 ,+∞).
,+∞).
点评:由于正切函数的值域为R,所以才能在R上求二次函数的值域.
则y=t2+t+1=(t+
 )2+
)2+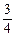 ≥
≥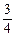 .
.∴原函数的值域是[
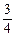 ,+∞).
,+∞).点评:由于正切函数的值域为R,所以才能在R上求二次函数的值域.

练习册系列答案
相关题目
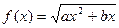 ,求满足下列条件的实数
,求满足下列条件的实数 的值:至少有一个正实数
的值:至少有一个正实数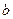 ,使函数
,使函数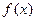 的定义域和值域相同。
的定义域和值域相同。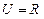 ,函数
,函数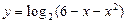 的定义域为A,函数
的定义域为A,函数 的定义域为B
的定义域为B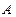 与
与 ;
;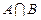 、
、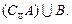
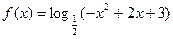
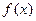 的定义域; (2)求
的定义域; (2)求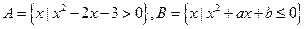 ,
,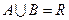 ,
,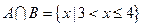 ,则
,则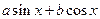 的最小值是多少?
的最小值是多少?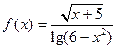 的定义域:
的定义域: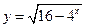 的值域是
的值域是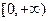
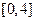

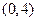
 的定义域
的定义域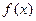 的定义域为
的定义域为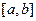 ,且
,且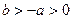 ,则函数
,则函数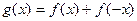 的定义域为_____________。
的定义域为_____________。