题目内容
已知函数f(x)是定义在R上的奇函数,且f(x)的图象关于直线x=1对称.
(1)求证:f(x)是周期为4的周期函数;
(2)若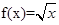 (0<x≤1),求x∈[-5,-4]时,函数f(x)的解析式.
(0<x≤1),求x∈[-5,-4]时,函数f(x)的解析式.
【答案】
(1)见解析;(2)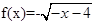 .
.
【解析】
试题分析:(1)只需证明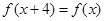 .由函数f(x)的图象关于直线
.由函数f(x)的图象关于直线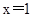 对称,可得
对称,可得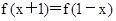 ,
,
即有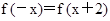 .根据函数
.根据函数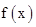 是定义在R上的奇函数,故有
是定义在R上的奇函数,故有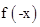 =-
=-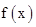 .
.
从而由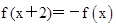 ,得到
,得到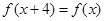 ,即f(x)是周期为4的周期函数.
,即f(x)是周期为4的周期函数.
(2)首先由函数f(x)是定义在R上的奇函数,得到f(0)=0.
根据x∈[-1,0)时,-x∈(0,1],f(x)=-f(-x)=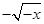 .
.
利用函数的周期性得到,x∈[-5,-4]时,函数f(x)的解析式.
试题解析:(1)证明:由函数f(x)的图象关于直线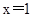 对称,有
对称,有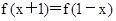 ,
,
即有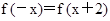 2分
2分
又函数f(x)是定义在R上的奇函数,故有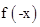 =-
=-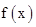 .
.
故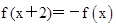 ,从而
,从而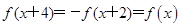 ,即
,即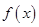 是周期为4的周期函数.
6分
是周期为4的周期函数.
6分
(2)由函数f(x)是定义在R上的奇函数,可知f(0)=0.
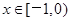 时,
时,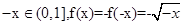 .
.
故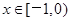 时,
时,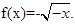 9分
9分
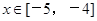 时,
时,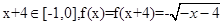 .
.
从而,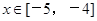 时,函数f(x)的解析式为
时,函数f(x)的解析式为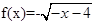 .
12分
.
12分
考点:函数的奇偶性、周期性

练习册系列答案
相关题目