题目内容
已知{an}是由非负整数组成的数列,满足a1=0,a2=3,an+1an=(an-1+2)(an-2+2),n=3,4,5,…,(1)求a3;
(2)证明an=an-2+2,n=3,4,5,…;
(3)求{an}的通项公式及其前n项和Sn.
分析:(1)由题设得a3a4=10,且a3、a4均为非负整数,所以a3的可能的值为1,2,5,10.然后逐个进行验证得a3=2.
(2)用数学归纳法进行证明,知对于所有k≥3,有ak+1=ak-1+2.
(3)由a2k-1=a2(k-1)-1+2,a1=0及a2k=a2(k-1)+2,a2=3,得a2k-1=2(k-1),a2k=2k+1,k=1,2,3,.
即an=n+(-1)n,n=1,2,3,所以Sn=
.
(2)用数学归纳法进行证明,知对于所有k≥3,有ak+1=ak-1+2.
(3)由a2k-1=a2(k-1)-1+2,a1=0及a2k=a2(k-1)+2,a2=3,得a2k-1=2(k-1),a2k=2k+1,k=1,2,3,.
即an=n+(-1)n,n=1,2,3,所以Sn=
|
解答:解:(1)由题设得a3a4=10,且a3、a4均为非负整数,所以a3的可能的值为1,2,5,10.
若a3=1,则a4=10,a5=
,与题设矛盾,
若a3=5,则a4=2,a5=
,与题设矛盾,
若a3=10,则a4=1,a5=60,a6=
,与题设矛盾,
所以a3=2.
(2)用数学归纳法证明,
①当n=3,a3=a1+2,等式成立,
②假设当n=k(k≥3)时等式成立,即ak=ak-2+2,
由题设ak+1ak=(ak-1+2)(ak-2+2),
∵ak=ak-2+2≠0,∴ak+1=ak-1+2,
也就是说,当n=k+1时,等式ak+1=ak-1+2成立.
根据①和②,对于所有k≥3,有ak+1=ak-1+2.
(3)由a2k-1=a2(k-1)-1+2,a1=0及a2k=a2(k-1)+2,a2=3,
得a2k-1=2(k-1),a2k=2k+1,k=1,2,3,
即an=n+(-1)n,n=1,2,3,
所以Sn=
若a3=1,则a4=10,a5=
| 3 |
| 2 |
若a3=5,则a4=2,a5=
| 35 |
| 2 |
若a3=10,则a4=1,a5=60,a6=
| 3 |
| 5 |
所以a3=2.
(2)用数学归纳法证明,
①当n=3,a3=a1+2,等式成立,
②假设当n=k(k≥3)时等式成立,即ak=ak-2+2,
由题设ak+1ak=(ak-1+2)(ak-2+2),
∵ak=ak-2+2≠0,∴ak+1=ak-1+2,
也就是说,当n=k+1时,等式ak+1=ak-1+2成立.
根据①和②,对于所有k≥3,有ak+1=ak-1+2.
(3)由a2k-1=a2(k-1)-1+2,a1=0及a2k=a2(k-1)+2,a2=3,
得a2k-1=2(k-1),a2k=2k+1,k=1,2,3,
即an=n+(-1)n,n=1,2,3,
所以Sn=
|
点评:本题考查数列的综合运用,解题时要仔细审题,要注意公式的灵活运用,注意答题的时间控制.

练习册系列答案
相关题目
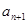 ,
,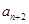 …的最小值记为Bn,dn=An-Bn.
…的最小值记为Bn,dn=An-Bn.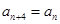 ),写出d1,d2,d3,d4的值;
),写出d1,d2,d3,d4的值;