题目内容
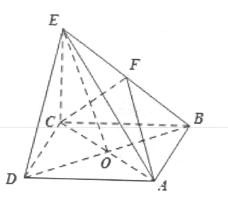
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,平面
,平面![]() 底面
底面![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 是棱
是棱![]() 上的点,
上的点,![]() ,
,![]() ,
,![]() .
.
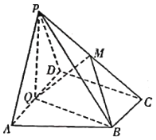
(1)若![]() 为
为![]() 的中点,求证:
的中点,求证:![]() 面
面![]() ;
;
(2)若二面角![]() 为
为![]() ,设
,设![]() ,试确定
,试确定![]() 的值.
的值.
【答案】(1)证明见解析 (2)![]()
【解析】
(1)连接![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() .证明
.证明![]() .利用直线与平面平行的判定定理证明
.利用直线与平面平行的判定定理证明![]() 平面
平面![]() .
.
(2)以![]() 为原点,
为原点,![]() 分别为
分别为![]() 轴建立空间直角坐标系.求出平面
轴建立空间直角坐标系.求出平面![]() 的法向量,平面
的法向量,平面![]() 法向量,利用二面角
法向量,利用二面角![]() 为
为![]() ,求解
,求解![]() 的值,得到答案.
的值,得到答案.
(1)证明:连接![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() .
.
∵![]() 且
且![]() ,
,
四边形![]() 为平行四边形,且
为平行四边形,且![]() 为
为![]() 中点,
中点,
又∵点![]() 是棱
是棱![]() 的中点,所以
的中点,所以![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
∴![]() 面
面![]() .
.
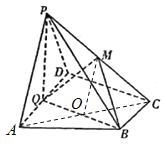
(2) ![]() ,
,![]() 为
为![]() 的中点,∴
的中点,∴![]() .
.
∵平面![]() 平面
平面![]() ,且平面
,且平面![]() ∩平面
∩平面![]() ,
,
∴![]() 平面
平面![]() .
.
∵![]() ,
,![]()
![]() 为
为![]() 的中点,∴四边形
的中点,∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]() .
.
∵![]() ,∴
,∴![]() 即
即![]()
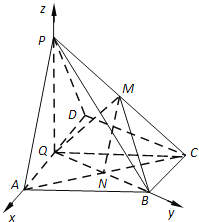
以![]() 为原点,
为原点,![]() 分别为
分别为![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
则![]()
则平面![]() 的法向量为
的法向量为![]()
设![]()
![]()
![]()
![]()
设平面![]() 的法向量为
的法向量为![]()
则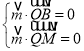 即
即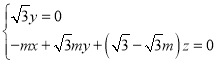
可取![]()
由二面角![]() 为
为![]()
所以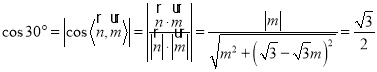
化简得:![]() ,解得:
,解得:![]() 或
或![]() (舍)
(舍)
所以![]() ,则
,则![]()
所以![]() .
.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
【题目】2022年第24届冬奥会将在中国北京和张家口举行,为了宣传冬奥会,某大学从全校学生中随机抽取了120名学生,对是否收看第23届平昌冬奥会开幕式情况进行了问卷调查,统计数据如下:
收看 | 没收看 | |
男生 | 60 | 20 |
女生 | 20 | 20 |
(1)根据上表数据,能否有![]() 的把握认为,收看开幕式与性别有关?
的把握认为,收看开幕式与性别有关?
(2)现从参与问卷调查且收看了开幕式的学生中,采用按性别分层抽样的方法选取8人,参加2022年北京冬奥会志愿者宣传活动,若从这8人中随机选取2人到较广播站开展冬奥会及冰雪项目宣传介绍,求恰好选到一名男生一名女生的概率.
附: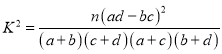 ,其中
,其中![]() .
.
P( | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |