题目内容
存在x∈R使得不等式x2-2x+k2-1≤0成立,则实数k的取值范围为
[-
,
]
| 2 |
| 2 |
[-
,
]
.| 2 |
| 2 |
分析:存在x∈R使得不等式x2-2x+k2-1≤0成立可转化成存在x∈R使得不等式x2-2x≤1-k2成立即(x2-2x)min≤1-k2,解不等式可求出所求.
解答:解:∵存在x∈R使得不等式x2-2x+k2-1≤0成立
∴存在x∈R使得不等式x2-2x≤1-k2成立即(x2-2x)min≤1-k2;
∵x2-2x=(x-1)2-1≥-1
∴-1≤1-k2即k2≤2
即k∈[-
,
]
故答案为:[-
,
]
∴存在x∈R使得不等式x2-2x≤1-k2成立即(x2-2x)min≤1-k2;
∵x2-2x=(x-1)2-1≥-1
∴-1≤1-k2即k2≤2
即k∈[-
| 2 |
| 2 |
故答案为:[-
| 2 |
| 2 |
点评:本题主要考查了一元二次不等式的应用,以及存在性问题的应用,同时考查了转化的思想,属于基础题.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
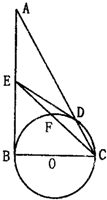 (选修4-1)如图,在△ABC中,∠ABC=90°,以BC为直径的圆O交AC于点D,设E为AB的中点.
(选修4-1)如图,在△ABC中,∠ABC=90°,以BC为直径的圆O交AC于点D,设E为AB的中点.