题目内容
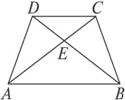
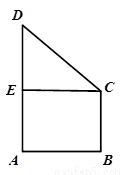
如图梯形ABCD,AD∥BC,∠A=900,过点C作CE∥AB,AD=2BC,AB=BC,,现将梯形沿CE
折成直二面角D-EC-AB.
(1)求直线BD与平面ABCE所成角的正切值;
(2)设线段AB的中点为 ,在直线DE上是否存在一点
,在直线DE上是否存在一点 ,使得
,使得 ∥面BCD?若存在,请指出点
∥面BCD?若存在,请指出点 的位置,并证明你的结论;若不存在,请说明理由;
的位置,并证明你的结论;若不存在,请说明理由;

【答案】
(1) (2)当
(2)当 为线段DE的中点时,PM∥平面BCD
为线段DE的中点时,PM∥平面BCD
【解析】
试题分析:(1)解:连接BE,因为梯形ABCD,∠A=900,CE∥AB,所以DE⊥EC
又 面DEC⊥面ABCE且交于EC ,
面DEC⊥面ABCE且交于EC , , 所以∠DBE为所求
, 所以∠DBE为所求
设BC=1,有AB="1" AD=2,所以DE="1"
EB=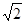 ,所以
,所以
(2)存在点 ,当
,当 为线段DE的中点时,PM∥平面BCD
为线段DE的中点时,PM∥平面BCD
取CD的中点N,连接BN,MN,则MN

 PB
PB
所以PMNB为平行四边形,所以PM∥BN
因为BN在平面BCD内,PM不在平面BCD内,所以PM∥平面BCD
考点:用空间向量求直线与平面的夹角;直线与平面平行的性质.
点评:本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,
以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
相关题目