题目内容
已知函数![]() 在
在![]() 处取得极小值.
处取得极小值.
(Ⅰ)若函数![]() 的极小值是
的极小值是![]() ,求
,求![]() ;
;
(Ⅱ)若函数![]() 的极小值不小于
的极小值不小于![]() ,问:是否存在实数k,使得函数
,问:是否存在实数k,使得函数![]() 在
在![]() 上单调递减.若存在,求出k的范围;若不存在,说明理由.
上单调递减.若存在,求出k的范围;若不存在,说明理由.
(Ⅰ)![]() ,由
,由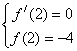
知![]() ,解得
,解得![]() , ……4分
, ……4分
检验可知,满足题意.![]() . ……6分
. ……6分
(Ⅱ)假设存在实数k,使得函数![]() 在
在![]() 上单调递减.
上单调递减.
设![]() =0两根为
=0两根为![]() ,则
,则![]()
由![]() 得
得![]()
![]()
![]() 的递减区间为
的递减区间为![]()
由![]() 解得
解得![]()
![]()
![]() 的递减区间为
的递减区间为![]()
由条件有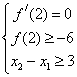 ,解得
,解得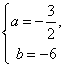 , ……10分
, ……10分
![]() 函数
函数![]() 在
在![]() 上单调递减
上单调递减
由![]()
![]()
![]()
![]()
所以,存在实数![]() ,满足题意。 ……12分
,满足题意。 ……12分

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
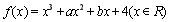
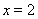
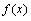

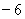



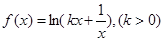 在
在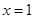 处取得极小值.
处取得极小值. 的值;
的值; 在
在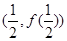 处的切线方程为
处的切线方程为 ,求证:当
,求证:当 时,曲线
时,曲线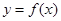 不可能在直线
不可能在直线 在
在 处取得极小值2.
处取得极小值2. 的解析式;
的解析式; ,若对于任意
,若对于任意 ,总存在
,总存在 ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围.