题目内容
已知函数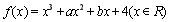 在
在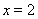 处取得极小值.
处取得极小值.
(1)若函数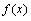 的极小值是
的极小值是 ,求
,求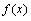 ;
;
(2)若函数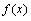 的极小值不小于
的极小值不小于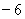 ,问:是否存在实数
,问:是否存在实数 ,使得函数
,使得函数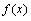 在
在 上单调递减?若存在,求出
上单调递减?若存在,求出 的范围;若不存在,说明理由.
的范围;若不存在,说明理由.
【答案】
(1)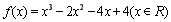 ;(2)存在实数
;(2)存在实数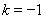 ,满足题意.
,满足题意.
【解析】
试题分析:(1)对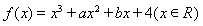 求导,得
求导,得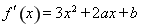 ,结合已知条件可以列出方程组
,结合已知条件可以列出方程组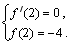 解这个方程组,可得
解这个方程组,可得 的值,从而求得
的值,从而求得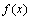 的解析式;(2)假设存在实数k,使得函数
的解析式;(2)假设存在实数k,使得函数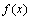 在
在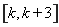 上单调递减.设
上单调递减.设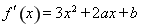 =0两根为
=0两根为 ,则
,则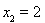 .由
.由 得
得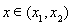 ,
,
 的递减区间为
的递减区间为 ,由
,由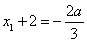 ,解得
,解得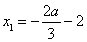 ,
,
 的递减区间为
的递减区间为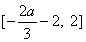 .由条件有
.由条件有 有这个条件组可求得
有这个条件组可求得 的值.利用函数
的值.利用函数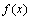 在
在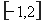 上单调递减,列出不等式组
上单调递减,列出不等式组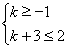 ,即可求得
,即可求得 的值.
的值.
试题解析:(1)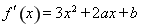 ,由
,由 知
知 ,
,
解得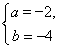 4分
4分
检验可知,满足题意.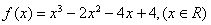 . 6分
. 6分
(2)假设存在实数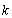 ,使得函数
,使得函数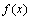 在
在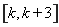 上单调递减.设
上单调递减.设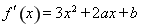 =0两根为
=0两根为 ,则
,则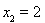 .由
.由 得
得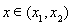 ,
,
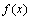 的递减区间为
的递减区间为 ,由
,由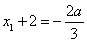 ,解得
,解得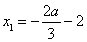 ,
,
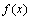 的递减区间为
的递减区间为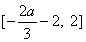 .
.
由条件有 ,解得
,解得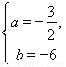 10分
10分
 函数
函数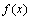 在
在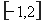 上单调递减.由
上单调递减.由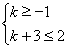
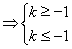
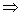
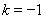 .∴存在实数
.∴存在实数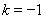 ,满足题意. 12分
,满足题意. 12分
考点:1.导数与函数的极值;2.导数与函数的单调性;3.含参数的探索性问题的解法.

练习册系列答案
相关题目
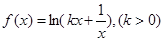 在
在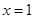 处取得极小值.
处取得极小值. 的值;
的值; 在
在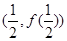 处的切线方程为
处的切线方程为 ,求证:当
,求证:当 时,曲线
时,曲线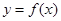 不可能在直线
不可能在直线 在
在 处取得极小值2.
处取得极小值2. 的解析式;
的解析式; ,若对于任意
,若对于任意 ,总存在
,总存在 ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围.