题目内容
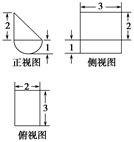
如图所示为一个几何体的直观图、三视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形).

(1)求四棱锥P-ABCD的体积;
(2)若G为BC上的动点,求证:AE⊥PG.

(1)求四棱锥P-ABCD的体积;
(2)若G为BC上的动点,求证:AE⊥PG.
(1) (2)见解析
(2)见解析
 (2)见解析
(2)见解析(1)由几何体的三视图可知,底面ABCD是边长为4的正方形,PA⊥平面ABCD,PA∥EB,且PA=4 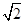 ,BE=2
,BE=2 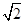 ,AB=4.∴VP-ABCD=
,AB=4.∴VP-ABCD= PA·S四边形ABCD=
PA·S四边形ABCD= ×4
×4 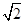 ×4×4=
×4×4= .
.
(2)∵ =
= ,∠EBA=∠BAP=90°,
,∠EBA=∠BAP=90°,
∴△EBA∽△BAP,∴∠BEA=∠PBA.
∴∠BEA+∠BAE=∠PBA+∠BAE=90°,∴PB⊥AE
又∵BC⊥平面APEB,∴BC⊥AE.∵BC∩PB=B,
∴AE⊥平面PBC.∵PG?平面PBC,∴AE⊥PG.
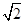 ,BE=2
,BE=2 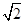 ,AB=4.∴VP-ABCD=
,AB=4.∴VP-ABCD= PA·S四边形ABCD=
PA·S四边形ABCD= ×4
×4 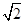 ×4×4=
×4×4= .
.(2)∵
 =
= ,∠EBA=∠BAP=90°,
,∠EBA=∠BAP=90°,∴△EBA∽△BAP,∴∠BEA=∠PBA.
∴∠BEA+∠BAE=∠PBA+∠BAE=90°,∴PB⊥AE
又∵BC⊥平面APEB,∴BC⊥AE.∵BC∩PB=B,
∴AE⊥平面PBC.∵PG?平面PBC,∴AE⊥PG.

练习册系列答案
相关题目




 各棱长均相等,
各棱长均相等, 分别为
分别为 中点,则
中点,则 在该四面体的面
在该四面体的面 上的射影是下图中的( )
上的射影是下图中的( )




 +4π cm2
+4π cm2


