��Ŀ����
��V��ȫ��ƽ���������ɵļ��ϣ���ӳ��f��V��R���㣺����������a=(x1��y1)��V��b=(x2��y2)��V���Լ�����ˡ�R������f(��a+(1-��)b)=��(a)+(1-��)f(b)�����ӳ��f��������P��
�ָ�������ӳ�䣺��f1��V��R��f1(m)=x-y��m=(x��y)��V��
��f2��V��R��f2(m)=x2+y��m=(x��y)��V��
��f3��V��R��f3(m)=x+y+1��m=(x��y)��V��
���У���������P��ӳ������Ϊ�� ������д�����о�������P��ӳ�����ţ�
�ָ�������ӳ�䣺��f1��V��R��f1(m)=x-y��m=(x��y)��V��
��f2��V��R��f2(m)=x2+y��m=(x��y)��V��
��f3��V��R��f3(m)=x+y+1��m=(x��y)��V��
���У���������P��ӳ������Ϊ�� ������д�����о�������P��ӳ�����ţ�
�٢�

��ϰ��ϵ�д�
 ��ʦ������Ԫ��ĩ���100��ϵ�д�
��ʦ������Ԫ��ĩ���100��ϵ�д� ��У������Ԫͬ��ѵ��������ϵ�д�
��У������Ԫͬ��ѵ��������ϵ�д�
�����Ŀ
 ���㣺����������
���㣺���������� �Լ�����
�Լ����� ��R������
��R������


 ���㣺����������
���㣺����������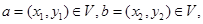 �Լ�����
�Լ����� ��R������
��R������

