题目内容
设V是全体平面向量构成的集合.若映射f:V→R满足:对任意向量a=(x1,y1)∈V,b=(x2,y2)∈V,以及任意λ∈R,均有f(λa+(1-λ)b)=λf(a)+(1-λ)f(b),则称映射f具有性质P.现给出如下映射:
①f1:V→R,f1(m)=x+y+1,m=(x,y)∈V;
②f2:V→R,f2(m)=x-y,m=(x,y)∈V;
③f3:V→R,f3(m)=x2+y,m=(x,y)∈V.
其中,具有性质P的映射的序号为
①f1:V→R,f1(m)=x+y+1,m=(x,y)∈V;
②f2:V→R,f2(m)=x-y,m=(x,y)∈V;
③f3:V→R,f3(m)=x2+y,m=(x,y)∈V.
其中,具有性质P的映射的序号为
(2)
(2)
.(写出所有具有性质P的映射的序号)分析:求出两个向量的和的坐标;分别对三个函数求f[λ a+(1-λ) b]与λf( a)+(1-λ)f( b)的值,判断哪个函数具有f[λ a+(1-λ) b]=λf( a)+(1-λ)f( b)即可.
解答:解:设 a=(x1,y1),b=(x2,y2),则λ a+(1-λ) b=(λx1+(1-λ)x2,λy1+(1-λ)y2),
对于①,f[λa+(1-λ)b]=λx1+(1-λ)x2+λy1+(1-λ)y2+1=λ(x1+y1)+(1-λ)(x2+y2)+1
而λf( a)+(1-λ)f( b)=λ(x1+y1+1)+(1-λ)(x2+y2+1)═λ(x1+y1)+(1-λ)(x2+y2)+1,
f1满足性质p;
对于②,f[λ a+(1-λ) b]=λx1+(1-λ)x2-λy1-(1-λ)y2=λ(x1-y1)+(1-λ)(x2-y2)
而λf( a)+(1-λ)f( b)=λ(x1-y1)+(1-λ)(x2-y2),f2满足性质P
对于③,f2(λa+(1-λb))=[λx1+(1-λ)x2]2+[λy1+(1-λ)y2],λf2(a)+(1-λ)f2(b)=λ(x12+y1)+(1-λ)(x22+y2)
∴f2(λa+(1-λb))≠λf2(a)+(1-λ)f2(b),∴映射f3不具备性质P.
故答案为:①②
对于①,f[λa+(1-λ)b]=λx1+(1-λ)x2+λy1+(1-λ)y2+1=λ(x1+y1)+(1-λ)(x2+y2)+1
而λf( a)+(1-λ)f( b)=λ(x1+y1+1)+(1-λ)(x2+y2+1)═λ(x1+y1)+(1-λ)(x2+y2)+1,
f1满足性质p;
对于②,f[λ a+(1-λ) b]=λx1+(1-λ)x2-λy1-(1-λ)y2=λ(x1-y1)+(1-λ)(x2-y2)
而λf( a)+(1-λ)f( b)=λ(x1-y1)+(1-λ)(x2-y2),f2满足性质P
对于③,f2(λa+(1-λb))=[λx1+(1-λ)x2]2+[λy1+(1-λ)y2],λf2(a)+(1-λ)f2(b)=λ(x12+y1)+(1-λ)(x22+y2)
∴f2(λa+(1-λb))≠λf2(a)+(1-λ)f2(b),∴映射f3不具备性质P.
故答案为:①②
点评:本题考查理解题中的新定义、考查利用映射的法则求出相应的像.

练习册系列答案
相关题目
 满足:对任意向量
满足:对任意向量 以及任意
以及任意 ∈R,均有
∈R,均有


 满足:对任意向量
满足:对任意向量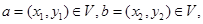 以及任意
以及任意 ∈R,均有
∈R,均有

