Question

已知使函数f（x）=x³-ax²+1（0≤a≤M₀）存在整数零点的实数a恰有3个，则M₀的取值范围是________．

Answer 1

．
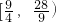分析：通过对a分类讨论，令f（x）=0，用x表示a，利用导数探究其单调性，找出取得整数零点的最小的三个、四个a 的值即可得出M₀的取值范围．
解答：①当a=0时，f（x）=x³+1=（x+1）（x²-x+1）存在一个整数零点-1，满足条件；
②当a≠0时，∵x=0时，f（0）=1≠0，∴0不是函数f（x）的零点；
由f（x）=x³-ax²+1=0（x≠0）可得，
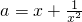令g（x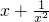）=，则=，
令g^′（x）=0，解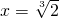得，列表得：
由表格可知：g（x）在区间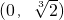上单调递减，
在区间（-∞，0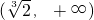），上单调递增，
画出图象：
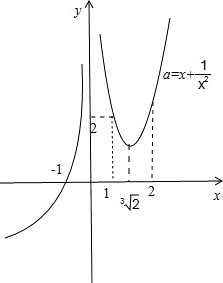当x＜0且x≠-1时，函数f（x）不存在零点；
当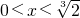时，只有一个整数零点x=1，此时a=2；
当x=时，不是整数零点应舍去；
当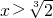时，最小整数零点x=2，此时a=；
比2大1的整数零点是3，此时a=．
综上可知：要满足函数f（x）=x³-ax²+1（0≤a≤M₀）存在整数零点的实数a恰有3个（即0，2，），则M₀的取值范围是．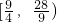
故答案为．
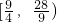点评：熟练掌握分类讨论的思想方法、利用导数探究函数的单调性是解题的关键．