题目内容
a从-1、1、2中任取一个数,b从-1、0、1中任取一个数.
(I)求函数f(x)=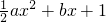 有零点的概率;
有零点的概率;
(II)求使两个不同向量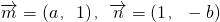 的夹角θ为锐角的概率.
的夹角θ为锐角的概率.
解:设点P(a,b),共有9个:(-1,-1),(-1,0),(-1,1),(1,-1),(1,0),(1,1),(2,-1),(2,0),(2,1).
(Ⅰ)记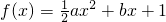 有零点为事件A.
有零点为事件A.
∵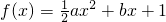 有零点,a≠0.
有零点,a≠0.
∴△≥0,化为b2≥2a,
故满足条件的(a,b)有3个,分别为(-1,-1),(-1,0),(-1,1).
∴概率P(A)= .
.
(2)记两个不同向量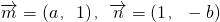 的夹角θ为锐角为事件B.
的夹角θ为锐角为事件B.
∴ ,化为
,化为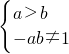 ,
,
故符合条件的P(a,b)共有4个:(1,0),(2,-1),(2,0),(2,1).
∴P(B)= .
.
分析:(1)先用列举法得出基本事件的总数,再根据二次函数有零点的充要条件即可得出函数f(x)=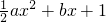 有零点的事件的个数,从而求出其概率;
有零点的事件的个数,从而求出其概率;
(2)两个不同向量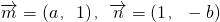 的夹角θ为锐角?
的夹角θ为锐角? ,解出即可.
,解出即可.
点评:根据具体问题正确求出基本事件和要求事件的个数是解题的关键.
(Ⅰ)记
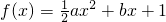 有零点为事件A.
有零点为事件A.∵
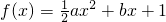 有零点,a≠0.
有零点,a≠0.∴△≥0,化为b2≥2a,
故满足条件的(a,b)有3个,分别为(-1,-1),(-1,0),(-1,1).
∴概率P(A)=
 .
.(2)记两个不同向量
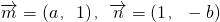 的夹角θ为锐角为事件B.
的夹角θ为锐角为事件B.∴
 ,化为
,化为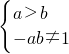 ,
,故符合条件的P(a,b)共有4个:(1,0),(2,-1),(2,0),(2,1).
∴P(B)=
 .
.分析:(1)先用列举法得出基本事件的总数,再根据二次函数有零点的充要条件即可得出函数f(x)=
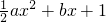 有零点的事件的个数,从而求出其概率;
有零点的事件的个数,从而求出其概率;(2)两个不同向量
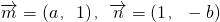 的夹角θ为锐角?
的夹角θ为锐角? ,解出即可.
,解出即可.点评:根据具体问题正确求出基本事件和要求事件的个数是解题的关键.

练习册系列答案
相关题目
从1.2.3.4.5中任取2个不同的数,事件A:“取到的2个数之和为偶数”,事件B:“取到的2个数均为偶数”,则P(B|A)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
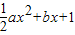 有零点的概率;
有零点的概率;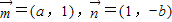 的夹角θ为锐角的概率.
的夹角θ为锐角的概率.