题目内容
已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5.(I)求抛物线G的方程;
(II)如图,过抛物线G的焦点的直线依次与抛物线G及圆x2+(y-1)2=1交于A、C、D、B四点,试证明|AC|•|BD|为定值;
(III)过A、B分别作抛物G的切线l1,l2且l1,l2交于点M,试求△ACM与△BDM面积之和的最小值.

【答案】分析:(1)第一小题较为简单,因为抛物线是标准方程,只须求参数P;
(2)直接推理、计算,并在计算过程中消去变量,从而得到定点;
(3)欲求面积之和的最小值,利用直线AB的斜率作为自变量,建立函数模型,转化成求函数的最值问题.
解答:解:(1)由题知,抛物线的准线方程为y+1=0,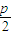 =1
=1
所以抛物线C的方程为x2=4y.
(2)设直线AB方y=kx+1交抛物线C于点A(x1,y1),B(x2,y2),
由抛物线定义知|AF|=y1+1,|BF|=y2+1,
所以|AC|=y1,|BD|=y2,
由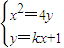 得x2-4kx-4=0,
得x2-4kx-4=0,
显然△>0,则x1+x2=4k,x1•x2=-4,
所以y1•y2=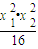 =1,所以|AC|•|BD|为定值1.
=1,所以|AC|•|BD|为定值1.
(3)解:由x2=4y,y= x2,y=
x2,y= x,
x,
得直线AM方程y-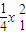 =
= x1(x-x1)(1),
x1(x-x1)(1),
直线BM方程y-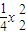 =
= x2(x-x2)(2),
x2(x-x2)(2),
由(2)-(1)得 (x1-x2)x=
(x1-x2)x=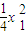 -
-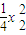 ,
,
所以x= (x1+x2)=2k,∴y=-1
(x1+x2)=2k,∴y=-1
所以点M坐标为(2k,-1),
点M到直线AB距离d=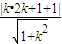 =2
=2 ,
,
弦AB长为|AB|=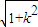
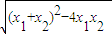 =
=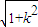
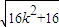 =4(1+k2),
=4(1+k2),
△ACM与△BDM面积之和,
S= (|AB|-2)•d=
(|AB|-2)•d= ×(2+4k2)×2
×(2+4k2)×2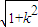 =2(1+2k2)
=2(1+2k2)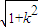 ,
,
当k=0时,即AB方程为y=1时,△ACM与△BDM面积之和最小值为2.
点评:新课标下的圆锥曲线题一般是压轴题,主要考查椭圆或抛物线的有关知识,本题主要考查直线、圆、抛物线等基础知识,考查运算求解能力、探究能力、分析问题和解决问题的能力,背景新颖,综合要求高.数学中的最值与定值问题,历来是高考的热点.求解定值与最值的基本策略有二:一是从几何角度考虑,当题目中的条件和结论明显体现几何特征及意义时,可用图形性质来解;二是从代数角度考虑,当题中的条件和结论体现出一种明显的函数关系时,可通过建立目标函数,求其目标函数的最值.
(2)直接推理、计算,并在计算过程中消去变量,从而得到定点;
(3)欲求面积之和的最小值,利用直线AB的斜率作为自变量,建立函数模型,转化成求函数的最值问题.
解答:解:(1)由题知,抛物线的准线方程为y+1=0,
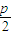 =1
=1所以抛物线C的方程为x2=4y.
(2)设直线AB方y=kx+1交抛物线C于点A(x1,y1),B(x2,y2),
由抛物线定义知|AF|=y1+1,|BF|=y2+1,
所以|AC|=y1,|BD|=y2,
由
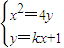 得x2-4kx-4=0,
得x2-4kx-4=0,显然△>0,则x1+x2=4k,x1•x2=-4,
所以y1•y2=
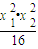 =1,所以|AC|•|BD|为定值1.
=1,所以|AC|•|BD|为定值1.(3)解:由x2=4y,y=
 x2,y=
x2,y= x,
x,得直线AM方程y-
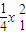 =
= x1(x-x1)(1),
x1(x-x1)(1),直线BM方程y-
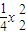 =
= x2(x-x2)(2),
x2(x-x2)(2),由(2)-(1)得
 (x1-x2)x=
(x1-x2)x=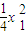 -
-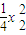 ,
,所以x=
 (x1+x2)=2k,∴y=-1
(x1+x2)=2k,∴y=-1所以点M坐标为(2k,-1),
点M到直线AB距离d=
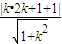 =2
=2 ,
,弦AB长为|AB|=
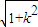
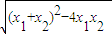 =
=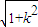
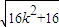 =4(1+k2),
=4(1+k2),△ACM与△BDM面积之和,
S=
 (|AB|-2)•d=
(|AB|-2)•d= ×(2+4k2)×2
×(2+4k2)×2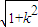 =2(1+2k2)
=2(1+2k2)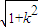 ,
,当k=0时,即AB方程为y=1时,△ACM与△BDM面积之和最小值为2.
点评:新课标下的圆锥曲线题一般是压轴题,主要考查椭圆或抛物线的有关知识,本题主要考查直线、圆、抛物线等基础知识,考查运算求解能力、探究能力、分析问题和解决问题的能力,背景新颖,综合要求高.数学中的最值与定值问题,历来是高考的热点.求解定值与最值的基本策略有二:一是从几何角度考虑,当题目中的条件和结论明显体现几何特征及意义时,可用图形性质来解;二是从代数角度考虑,当题中的条件和结论体现出一种明显的函数关系时,可通过建立目标函数,求其目标函数的最值.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
(本小题满分15分)
已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5。
(I)求抛物线G的方程;
(II)如图,过抛物线G的焦点的直线依次与抛物线G及圆![]() 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明![]() 为定值;
为定值;
|
 已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5.
已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5.

