题目内容
18.集合A={x|x2-2x-3<0},B={x|x2<p},若B?A,则实数p的取值范围是( )| A. | (0,1] | B. | (-∞,1] | C. | (-1,3] | D. | (-∞,1) |
分析 首先,化简集合A,然后,分两种情况:当B=∅时,和当B≠∅时,进行讨论完成即可.
解答 解:A={x|x2-2x-3<0}
={x|-1<x<3},
当B=∅时,即p≤0时显然成立,
当B≠∅时,即p>0时,
∴B={x|-$\sqrt{p}$<x<$\sqrt{p}$},
∵B?A,
∴$\left\{\begin{array}{l}{\sqrt{p}≤3}\\{-\sqrt{p}≥-1}\end{array}\right.$,
∴0<p≤1,
综上,实数p的取值范围是(-∞,1].
故选:B.
点评 本题重点考查了集合的基本运算性质等知识,属于中档题.

练习册系列答案
相关题目
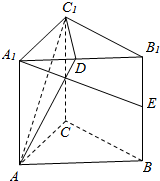 如图,在直三棱柱ABC-A1B1C1中,AC=BC,侧面BB1A1是正方形,D,E分别为A1B1和BB1的中点.求证:A1E⊥平面AC1D.
如图,在直三棱柱ABC-A1B1C1中,AC=BC,侧面BB1A1是正方形,D,E分别为A1B1和BB1的中点.求证:A1E⊥平面AC1D.