题目内容
某地区的一种特色水果上市时间能持续5个月，预测上市初期和后期会因供不应求使价格呈连续上涨态势，而中期又将出现供大于求使价格连续下跌现象，现有三种价格模拟函数：
①
=
；②=
；
③=
．(以下三式中
、
均为常数，且>2)
(1)为准确研究其价格走势，应选哪种价格模拟函数，为什么?
(2)若
=4，
=6，求出所选函数的解析式(注：函数的定义域是[1，6]．其中
=1表示4月1日，=2表示5月1日……以此类推)．
(3)试问：在(2)的条件下，这种水果在几月份价格下跌?
解：(1)因为①，
是单调函数；②
是单调函数；③
中，
，令
0，得
，
．
有两个零点，
可以出现两个递增区间和一个递减区间．
所以应选为模拟函数．
(2)由
(1)=4，(3)=6得
，(其中q=2舍去)．
∴(
)=(－1)(－4)2+4=3－92+24－12，(1≤≤6)．
(3)由
()=32―18+24<0，解得2<<4，
∴函数()=3－92+24－12在区间(2，4)单调递减，
∴这种水果在5月份、6月份价格下跌．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
某地区的一种特色水果上市时间仅能持续几个月，预测上市初期和后期会因供不应求使价格呈连续上涨的态势，而中期又将出现供大于求使价格连续下跌，为准确研究其价格走势，下面给出四个价格模拟函数中适合的是（其中为p、q常数，0＜q＜4，且x∈（0，5））（ ）
| A、f（x）=p•qx | B、f（x）=px2+qx+1 | C、f（x）=plnx+qx2 | D、f（x）=x（x-q）2+p |
；②
；③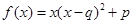
．（以上三式中
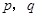均为常数，且
）
，
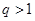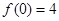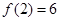，求出所选函数
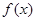的解析式（注：函数的定义域是
）．其中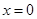
表示4月1日，
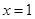表示5月1日，…，依此类推；