题目内容

设f（x）=|x|，则
∫
2
-2
f(x)dx=
4
4
．
分析：解题的关键是利用被积函数是偶函数，得到
∫
2
-2
f(x)dx=2∫
 
2
0
f（x）dx，从而解决问题．
解答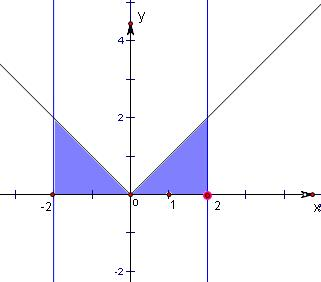：解：∵f（x）是偶函数，
故其图象关于y轴对称，
根据定积分的几何意义是函数图象与x轴所围成的封闭图形的面积的代数和，知
函数f（x）在区间[-2，2]上的图象必定关于y轴对称，
从而函数图象与x轴所围成的封闭图形的面积在y轴的左右两边的值相等，
故
∫
2
-2
f(x)dx=2∫
 
2
0
f（x）dx=2∫02xdx=4．
故答案为：4．
点评：本题主要考查了偶函数的性质、定积分及定积分的应用．属于基础题．
练习册系列答案
相关题目
设函数f（x）=a2x2（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为
2
，求a的值；
（2）关于x的不等式（x-1）2＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=
2
2
，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．
设函数f（x）=a2x2（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为2
2
，求a的值；
（2）关于x的不等式（x-1）2＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=
2
2
，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．
设f（x），g（x），h（x）是R上的任意实值函数，如下定义两个函数（f°g）（x）和（x）对任意x∈R，（f°g）（x）=f（g（x））；（x）=f（x）g（x），则下列等式恒成立的是（ ）
A．（（f°g）•h）（x）=°）（x）
B．°h）（x）=（（f°h）•（g°h））（x）
C．（（f°g）°h）（x）=（（f°h）°（g°h））（x）
D．•h）（x）=•）（x）
设f（x），g（x），h（x）是R上的任意实值函数，如下定义两个函数（f°g）（x）和（x）对任意x∈R，（f°g）（x）=f（g（x））；（x）=f（x）g（x），则下列等式恒成立的是（ ）
A．（（f°g）•h）（x）=°）（x）
B．°h）（x）=（（f°h）•（g°h））（x）
C．（（f°g）°h）（x）=（（f°h）°（g°h））（x）
D．•h）（x）=•）（x）
设f（x），g（x），h（x）是R上的任意实值函数，如下定义两个函数（f°g）（x）和（x）对任意x∈R，（f°g）（x）=f（g（x））；（x）=f（x）g（x），则下列等式恒成立的是（ ）
A．（（f°g）•h）（x）=°）（x）
B．°h）（x）=（（f°h）•（g°h））（x）
C．（（f°g）°h）（x）=（（f°h）°（g°h））（x）
D．•h）（x）=•）（x）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网