题目内容

已知O、A、B是平面上的三点，向量
O
A=
a
，
O
B=
b
，在平面AOB上，P为线段AB的垂直平分线上任一点，向量
OP
=
p
且|
a
|=3， |
b
|=2，则
p
•(
a
-
b
)值是（　　）
A、
5
2
B、5
C、3
D、
3
2
分析：由已知中向量
O
A=
a
，
O
B=
b
，在平面AOB上，P为线段AB的垂直平分线上任一点，我们易根据两垂直向量数量积为零，及向量加减法的三角形法则，易得到答案．
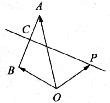解答：精英家教网解：设C点为AB的中点，P为线段AB的垂直平分线上任一点
∵
O
A=
a
，
O
B=
b
，
O
A=
a
，
O
B=
b
，
p
•(
a
-
b
)=
OP
•(
OA
-
OB
)
=(
OC
+
CP
)•
BA
=
OC
•
BA

=
1
2
(
a
+
b
)•(
a
-
b
)
=
1
2
(
a
2-
b
2)=
5
2

故选A
点评：本题考查的知识点是平面向量的数量积的运算，其中根据P为线段AB的垂直平分线上任一点，得到CP与AB垂直，其对应的向量数量积为零是解答本题的关键．
练习册系列答案
相关题目
已知O，A，B是平面上的三个点，直线AB上有一点C，满足2
AC
+
CB
=0，则
OC
等于（　　）
A、2
OA
-
OB
B、-
OA
+2
OB
C、
2
3
OA
-
1
3
OB
D、-
1
3
OA
+
2
3
OB
已知O，A，B是平面上的三个点，直线AB上有一点C，满足2
AC
+
CB
=
0
，则
OC
=
2
OA
-
OB
2
OA
-
OB
（要求用
OA
，
OB
表示）
已知O、A、B是平面上三点，直线AB上有一点C满足3
AC
+2
CB
=
0
，则
OC
等于（　　）
已知O，A，B是平面上的三点，向量
OA
=
a
.
OB
=
b
，点C是线段AB的中点，设P为线段AB的垂直平分线CP上任意一点，向量
OP
=
P
，若|
a
|=4，|
b
|=2，则
p
•(
a
-
b
)=
6
6
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网