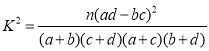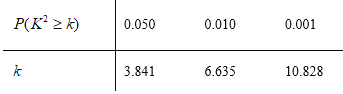题目内容
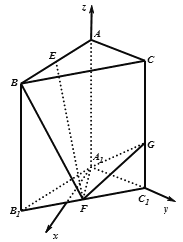
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 中点,
中点,![]() 为线段
为线段![]() 上的一个动点.
上的一个动点.
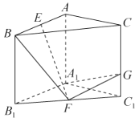
(1)证明:![]() 平面
平面![]() ;
;
(2)当二面角![]() 的余弦值为
的余弦值为![]() 时,证明:
时,证明:![]() .
.
【答案】(1)证明见解析.(2)证明见解析
【解析】
(1)取![]() 中点
中点![]() ,连
,连![]() ,可证四边形
,可证四边形![]() 为平行四边形,得到
为平行四边形,得到![]() ,即可证明结论;
,即可证明结论;
(2)不妨设![]() ,如下图建立空间直角坐标系
,如下图建立空间直角坐标系![]() ,设
,设![]() ,得到
,得到![]() 坐标, 求出平面
坐标, 求出平面![]() 的法向量坐标,取平面
的法向量坐标,取平面![]() 法向量为
法向量为![]() ,根据已知求出
,根据已知求出![]() ,证明
,证明![]() 即可.
即可.
(1)如图,取![]() 中点
中点![]() ,连
,连![]() ,
,
因为![]() 是
是![]() 的中点,所以
的中点,所以![]() ,
,
在直三棱柱![]() 中,
中,![]() ,
,
因为![]() 是
是![]() 中点,所以
中点,所以![]() ,
,
所以四边形![]() 为平行四边形,
为平行四边形,![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ;
;
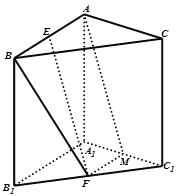
(2)不妨设![]() ,如图建立空间直角坐标系
,如图建立空间直角坐标系![]() ,
,
设![]() ,
, ,
, ,
,![]() ,
,
所以![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则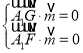 ,即
,即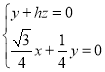 ,令
,令![]() ,
,
所以平面![]() 的一个法向量
的一个法向量![]() ,
,
平面![]() 的一个法向量
的一个法向量![]() ,
,
所以![]() ,
,
此时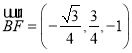 ,
,![]() ,
,
所以![]() ,即
,即![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】在传染病学中,通常把从致病刺激物侵人机体或者对机体发生作用起,到机体出现反应或开始呈现该疾病对应的相关症状时止的这一阶段称为潜伏期. 一研究团队统计了某地区1000名患者的相关信息,得到如下表格:
潜伏期(单位:天) |
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
(1)求这1000名患者的潜伏期的样本平均数x (同一组中的数据用该组区间的中点值作代表) ;
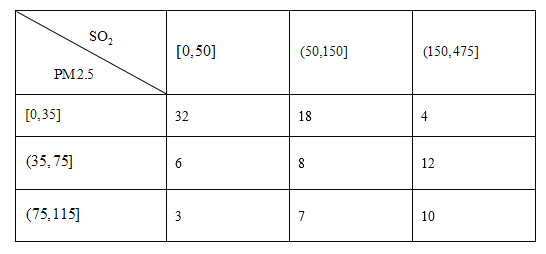
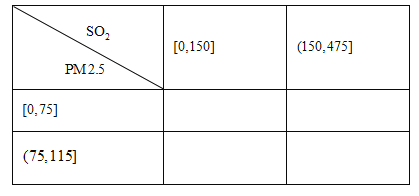
(2)该传染病的潜伏期受诸多因素的影响,为研究潜伏期与患者年龄的关系,以潜伏期是否超过6天为标准进行分层抽样,从上述1000名患者中抽取200人,得到如下列联表
潜伏期 | 潜伏期 | 总计 | |
|
| ||
|
| ||
总计 |
|
(3)以这1000名患者的潜伏期超过6天的频率,代替该地区1名患者潜伏期超过6天发生的概率,每名患者的潜伏期是否超过6天相互独立,为了深入研究,该研究团队随机调查了20名患者,其中潜伏期超过6天的人数最有可能(即概率最大)是多少?
附:
|
|
|
|
|
|
|
|
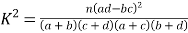 ,其中
,其中![]() .
.
【题目】垃圾分类是对垃圾进行有效处置的一种科学管理方法.太原市为推进这项工作的实施,开展了“垃圾分类进小区”的评比活动.现有甲、乙两个小区采取不同的宣传与倡导方式对各自小区居民进行了有关垃圾分类知识的培训,并参加了评比活动,评委会随机从两个小区各选出20户家庭进行评比打分,每户成绩满分为100分,评分后得到如下茎叶图.
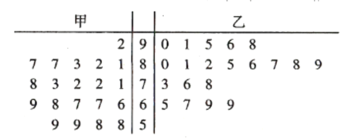
(1)依茎叶图判断哪个小区的平均分高?
(2)现从甲小区不低于80分的家庭中随机抽取两户,求分数为87的家庭至少有一户被抽中的概率;
(3)如果规定分数不低于85分的家庭为优秀,请填写下面的![]() 列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为得分是否优秀与小区宣传培训方式有关?”
列联表,并判断“能否在犯错误的概率不超过0.025的前提下认为得分是否优秀与小区宣传培训方式有关?”
甲 | 乙 | 合计 | |
优秀 |
|
| |
不优秀 |
|
| |
合计 |
参考公式和数据: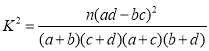 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |