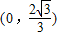题目内容
已知椭圆的内接三角形有一个顶点在短轴的顶点处,其重心是椭圆的一个焦点,求该椭圆离心率e的取值范围.
- A.
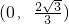
- B.
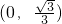
- C.
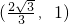
- D.
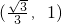
B
分析:设出椭圆方程,根据其内接三角形的一个顶点是短轴的一个顶点,重心是一个焦点,利用向量求出已知顶点对边的中点,由该中点在椭圆内部列式求椭圆离心率的范围.
解答:不防设椭圆方程: (a>b>0),
(a>b>0),
再不妨设:B(0,b),三角形重心G(c,0),
延长BG至D,使|GD|= ,
,
设D(x,y),则 ,
, ,
,
由 ,得:
,得: ,
,
解得: ,
,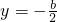 .
.
而D 是椭圆的内接三角形一边AC的中点,
是椭圆的内接三角形一边AC的中点,
所以,D点必在椭圆内部,
则 .
.
把b2=a2-c2代入上式整理得: .
.
即 .
.
又因为椭圆离心率e∈(0,1),
所以,该椭圆离心率e的取值范围是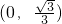 .
.
故选B.
点评:本题考查了椭圆的简单几何性质,考查了椭圆离心率的求法,求椭圆离心率范围的关键是利用椭圆的性质及平面几何知识,找到含有a和c的不等式.此题是中档题.
分析:设出椭圆方程,根据其内接三角形的一个顶点是短轴的一个顶点,重心是一个焦点,利用向量求出已知顶点对边的中点,由该中点在椭圆内部列式求椭圆离心率的范围.
解答:不防设椭圆方程:
 (a>b>0),
(a>b>0),再不妨设:B(0,b),三角形重心G(c,0),
延长BG至D,使|GD|=
 ,
,设D(x,y),则
 ,
, ,
,由
 ,得:
,得: ,
,解得:
 ,
,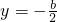 .
.而D
 是椭圆的内接三角形一边AC的中点,
是椭圆的内接三角形一边AC的中点,所以,D点必在椭圆内部,
则
 .
.把b2=a2-c2代入上式整理得:
 .
.即
 .
.又因为椭圆离心率e∈(0,1),
所以,该椭圆离心率e的取值范围是
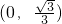 .
.故选B.
点评:本题考查了椭圆的简单几何性质,考查了椭圆离心率的求法,求椭圆离心率范围的关键是利用椭圆的性质及平面几何知识,找到含有a和c的不等式.此题是中档题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目