题目内容
对于下列命题:①在△ABC中,若 ,则△ABC为等腰三角形;②已知a, b,c是△ABC的三边长,若
,则△ABC为等腰三角形;②已知a, b,c是△ABC的三边长,若 ,
, ,
, ,则△ABC有两组解;③设
,则△ABC有两组解;③设 ,
,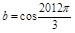 ,
, ,则
,则 ;④将函数
;④将函数 图象向左平移
图象向左平移 个单位,得到函数
个单位,得到函数 图象。其中正确命题的个数是 .
图象。其中正确命题的个数是 .
 ,则△ABC为等腰三角形;②已知a, b,c是△ABC的三边长,若
,则△ABC为等腰三角形;②已知a, b,c是△ABC的三边长,若 ,
, ,
, ,则△ABC有两组解;③设
,则△ABC有两组解;③设 ,
,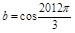 ,
, ,则
,则 ;④将函数
;④将函数 图象向左平移
图象向左平移 个单位,得到函数
个单位,得到函数 图象。其中正确命题的个数是 .
图象。其中正确命题的个数是 . (3)(4)
试题分析:①,∵△ABC中,若sin2A=sin2B,∴2A=2B或2A+2B=π,∴△ABC为等腰三角形或直角三角形,故①错误;
②,∵a,b,c是△ABC的三边长,若a=2,b=5,A=
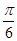 ,
,∴由正弦定理得,
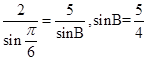 >1,这是不可能的,故②错误;
>1,这是不可能的,故②错误;③,∵
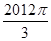 =335×2π+
=335×2π+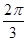 ,∴
,∴ =sin
=sin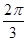 =
=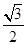 ,同理可得b=cos
,同理可得b=cos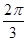 =-
=-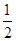 ,c=tan
,c=tan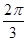 =-
=-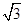 ,故a>b>c,③正确;
,故a>b>c,③正确;④将函数
 图象向左平移
图象向左平移 个单位,得:y=2sin[3(x+
个单位,得:y=2sin[3(x+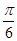 )+
)+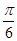 ]
]=2sin[
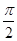 +(3x+
+(3x+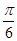 )]=
)]= ,故④正确;
,故④正确;故答案为(3)(4)。
点评:中档题,根据三角函数的性质与正弦定理对四个结论逐一进行判断,即可得到正确的结论。说明结论不成立,也可以通过选取特殊值,举反例。

练习册系列答案
相关题目
 ,
, ,则边b=
,则边b=  中,已知
中,已知


 求A的值.
求A的值.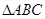 中,若
中,若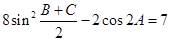 。
。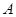 的大小;
的大小;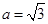 ,
,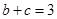 ,求
,求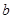 ,
,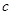 的值。
的值。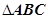 中,AD为BC边上的中线,且AC=2AB=2AD=4,则BD=________.
中,AD为BC边上的中线,且AC=2AB=2AD=4,则BD=________.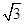 ,BC=2,C=60°,则边AB的长度等于________.
,BC=2,C=60°,则边AB的长度等于________. 中,
中, 分别是三内角
分别是三内角 的对边,设
的对边,设
 ,则
,则 ( )
( ) 或
或
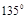
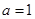 ,
, ,则最大边
,则最大边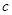 的取值范围是 。
的取值范围是 。 中,内角A、B、C的对边分别是
中,内角A、B、C的对边分别是 、b、c,已知
、b、c,已知 ,且
,且 的夹角为
的夹角为 。
。 ,三角形的面积
,三角形的面积 ,求
,求 的值。
的值。