题目内容
设函数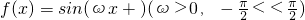 ,给出以下四个论断:
,给出以下四个论断:
①它的图象关于直线 对称;
对称;
②它的图象关于点( ,0)对称;
,0)对称;
③它的最小正周期是π;
④在区间[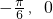 ]上是增函数.
]上是增函数.
以其中两个论断作为条件,余下论断作为结论,一个正确的命题:
条件 ______________,结论 ______________.
- A.①②?③④
- B.③④?①②
- C.②④?①③
- D.①③?②④
D
分析:由③知ω=2,再由对称轴,可得函数解析式,再求出函数的单调区间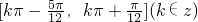 ,因为
,因为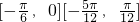 可得f(x)在区间[
可得f(x)在区间[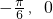 ]上是增函数,得到结论.
]上是增函数,得到结论.
解答:①③?②④
由③知ω=2
∴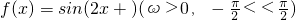
又由①2× +φ=kπ+
+φ=kπ+
∴φ=kπ+
又∵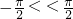
∴φ=
∴
∵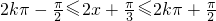
∴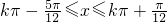
∵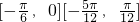
∴f(x)在区间[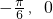 ]上是增函数
]上是增函数
故选D
点评:本题主要考查三角函数的周期性,单调性,对称性,以及学生构造命题拓展问题的能力.
分析:由③知ω=2,再由对称轴,可得函数解析式,再求出函数的单调区间
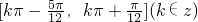 ,因为
,因为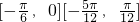 可得f(x)在区间[
可得f(x)在区间[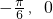 ]上是增函数,得到结论.
]上是增函数,得到结论.解答:①③?②④
由③知ω=2
∴
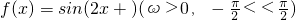
又由①2×
 +φ=kπ+
+φ=kπ+
∴φ=kπ+

又∵
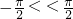
∴φ=

∴

∵
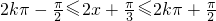
∴
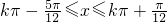
∵
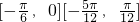
∴f(x)在区间[
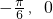 ]上是增函数
]上是增函数故选D
点评:本题主要考查三角函数的周期性,单调性,对称性,以及学生构造命题拓展问题的能力.

练习册系列答案
相关题目
 ,给出以下四个论断:
,给出以下四个论断: 对称;
对称;  对称;
对称;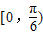 上是增函数.
上是增函数.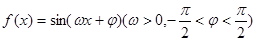 ,给出以下四个论断:
,给出以下四个论断: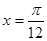 对称; ③它的最小正周期是
对称; ③它的最小正周期是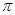 ;
; ,0)对称;④在区间[
,0)对称;④在区间[ ]上是增函数.
]上是增函数.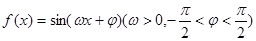 ,给出以下四个论断:
,给出以下四个论断: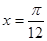 对称; ③它的最小正周期是
对称; ③它的最小正周期是 ;
;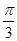 ,0)对称;
④在区间[
,0)对称;
④在区间[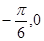 ]上是增函数.
]上是增函数.