题目内容
(2007•南通模拟)方程x2+1=2x的解共有( )
分析:在同一平面坐标系中画出函数f(x)=x2+1,g(x)=2x的图象,根据二次函数和指数函数的性质,分析出两个函数图象交点的个数,即方程x2+1=2x的解的个数.
解答:解:方程x2+1=2x的解的个数等于函数(x)=x2+1,g(x)=2x交的个数
在同一平面坐标系中画出函数f(x)=x2+1,g(x)=2x的图象如下图所示
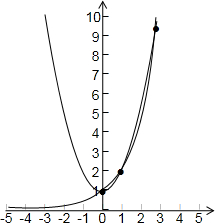
由于两个函数的图象共有3个交点
故方程x2+1=2x的解共有3个
故选C
在同一平面坐标系中画出函数f(x)=x2+1,g(x)=2x的图象如下图所示

由于两个函数的图象共有3个交点
故方程x2+1=2x的解共有3个
故选C
点评:本题考查的知识点是函数的零点与方程根的关系,其中利用转化思想,将求方程x2+1=2x的解的个数,转化为判断函数f(x)=x2+1,g(x)=2x的图象交点的个数,是解答本题的关键.

练习册系列答案
相关题目