题目内容
1.设关于x、y的不等式组$\left\{\begin{array}{l}{3x-4≥0}\\{(y-1)(3x+y-6)≤0}\end{array}\right.$表示的平面区域为D,已知点O(0,0)、A(1,0),点M是D上的动点,$\overrightarrow{OA}$$•\overrightarrow{OM}$=λ|$\overrightarrow{OM}$|,则λ的取值范围是($\frac{\sqrt{10}}{10}$,1].分析 先画出不等式组所表示的平面区域D,而由$\overrightarrow{OA}•\overrightarrow{OM}=λ|\overrightarrow{OM}|$便可得到,λ=cos∠MOA,所以求cos∠MOA的取值范围即可,通过图形找出∠MOA的变化过程,从而便可求得cos∠MOA的变化范围.
解答 解:由不等式组 $\left\{\begin{array}{l}{3x-4≥0}\\{(y-1)(3x+y-6)≤0}\end{array}\right.$得:
$\left\{\begin{array}{l}{x≥\frac{4}{3}}\\{y≥1}\\{y≤-3x+6}\end{array}\right.$,或$\left\{\begin{array}{l}{x≥\frac{4}{3}}\\{y≤1}\\{y≥-3x+6}\end{array}\right.$;
∴平面区域D如下图阴影部分所示: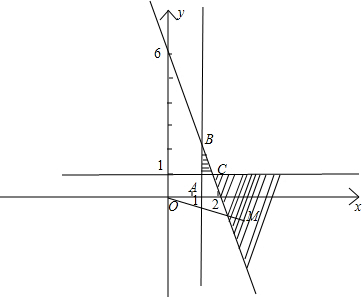
由$\overrightarrow{OA}•\overrightarrow{OM}=λ|\overrightarrow{OM}|$得,λ=cos∠MOA;
如图所示,若设直线x=$\frac{4}{3}$和y=-3x+6的交点为B,则B点坐标为($\frac{4}{3}$,2),所以|OB|=$\frac{2\sqrt{13}}{3}$,
当M点从B点开始向x轴靠近的过程中,∠MOA不断减小,并减小到0,当∠MOA=0°时对应的λ的值达到最大值,
而当M从x轴并在阴影部分远离x轴时,∠MOA又逐渐增大,可知∠MOA的最大值(极限值)一定在直线y=-3x+6上取得,比较此极限值和M在B点对应的λ值即可求出λ的最小值;
当M点在B点时,cos∠MOA=$\frac{\frac{4}{3}}{\frac{2\sqrt{13}}{3}}$=$\frac{2\sqrt{13}}{13}$;
当M点在第四象限且在直线上时,设M(x,-3x+6),则cos∠MOA=$\frac{x}{{x}^{2}+(-3x+6)^{2}}$,
当x趋近于正无穷时,cos∠MOA=$\frac{\sqrt{10}}{10}$,
∵$\frac{2\sqrt{13}}{13}$>$\frac{\sqrt{10}}{10}$;
∴λ的取值范围是($\frac{\sqrt{10}}{10}$,1].
故答案为:($\frac{\sqrt{10}}{10}$,1].
点评 考查不等式组表示平面区域的概念,能根据不等式组找出不等式组所表示的平面区域,数量积的计算公式,以及余弦函数的单调性,向量夹角的定义,数形结合解题的方法.

| A. | $\overrightarrow{{e}_{1}}$=(0,0),$\overrightarrow{{e}_{2}}$=(2,1) | B. | $\overrightarrow{{e}_{1}}$=(3,4),$\overrightarrow{{e}_{2}}$=(6,8) | ||
| C. | $\overrightarrow{{e}_{1}}$=(-1,2),$\overrightarrow{{e}_{2}}$=(3,-2) | D. | $\overrightarrow{{e}_{1}}$=(1,-3),$\overrightarrow{{e}_{2}}$=(-1,3) |
| A. | $\sqrt{2}-1$ | B. | 2 | C. | $\sqrt{2}+1$ | D. | $2\sqrt{2}$ |
| A. | (0,3) | B. | (1,1) | C. | (2,4) | D. | (2,5) |
 如图,在斜三棱柱ABC-A1B1C1中,O是AC的中点,A1O⊥平面ABC,∠BCA=90°,AA1=AC=BC.
如图,在斜三棱柱ABC-A1B1C1中,O是AC的中点,A1O⊥平面ABC,∠BCA=90°,AA1=AC=BC.