题目内容
从装有10个大小相同的小球(4个红球、3个白球、3个黑球)口袋中任取两个,则取出两个同色球的概率是( )A.
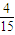
B.
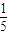
C.

D.

【答案】分析:根据题意,首先求得从10个球中,任取两个的情况数目,进而分别求得取出的球都是红色、白色、黑色的情况数目,进而可得取出两个同色球的数目,由古典概型公式计算可得答案.
解答:解:根据题意,从10个球中,任取两个,有C102=45种不同的取法,
取出的球同是红球的有C42=6种,
取出的球同是白球的有C32=3种,
取出的球同是黑球的有C32=3种,
则取出两个同色球的情况有6+3+3=12种,
故其概率为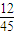 =
=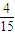 .
.
点评:本题考查互斥事件、相互独立事件的概率计算,注意分类讨论的运用.
解答:解:根据题意,从10个球中,任取两个,有C102=45种不同的取法,
取出的球同是红球的有C42=6种,
取出的球同是白球的有C32=3种,
取出的球同是黑球的有C32=3种,
则取出两个同色球的情况有6+3+3=12种,
故其概率为
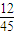 =
=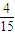 .
.点评:本题考查互斥事件、相互独立事件的概率计算,注意分类讨论的运用.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
从装有10个大小相同的小球(4个红球、3个白球、3个黑球)口袋中任取两个,则取出两个同色球的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|



