题目内容
若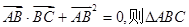 是 ( )
是 ( )
| A.锐角三角形 | B.直角三角形 | C.钝角三角形 | D.等腰直角三角形 |
B
解析试题分析:∵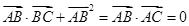 ,∴
,∴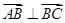 ,即∠A=
,即∠A= ,故
,故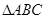 为直角三角形,故选B
为直角三角形,故选B
考点:本题考查了数量积的运算及三角形形状的判断
点评:熟练运用向量的运算及数量积的含义来判断三角形中的边角关系是解决此类问题的关键

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
已知单位向量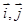 满足
满足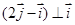 ,则
,则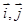 夹角为( )
夹角为( )
A.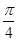 | B.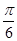 | C. | D.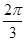 |
已知平面向量a、b均为单位向量,且a与b的夹角为1200,则|2a+b|=( )
| A.3 | B.7 | C.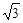 | D. |
定义平面向量之间的一种运算“⊙”如下:对任意的a=(m,n),b=(p,q),令a⊙b= mq
-np,下面说法错误的是( )
| A.若a与b共线,则a⊙b =0 |
| B.a⊙b =b⊙a |
C.对任意的 R,有( R,有(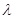 a)⊙b = a)⊙b =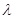 (a⊙b) (a⊙b) |
| D.(a⊙b)2+(a·b)2= |a|2|b|2 |
已知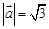 ,
,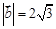 ,
,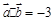 ,则
,则 与
与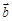 的夹角是
的夹角是
A.30 | B.60 | C.120 | D.150 |
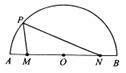
如图,AB是圆O的直径,P是圆弧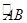 上的点,M,N是直径AB上关于O对称的两点,且
上的点,M,N是直径AB上关于O对称的两点,且 ,则
,则
| A.13 | B.7 | C.5 | D.3 |
已知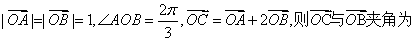
A.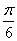 | B. | C.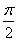 | D.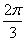 |
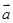 ,
,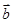 ,
,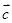 是空间任意的非零向量,且相互不共线,则以下命题中:
是空间任意的非零向量,且相互不共线,则以下命题中: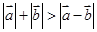 ;③
;③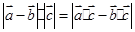 .
.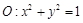 和三点,
和三点, ,
,
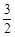 B.
B. C.
C.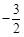 D.
D.