题目内容
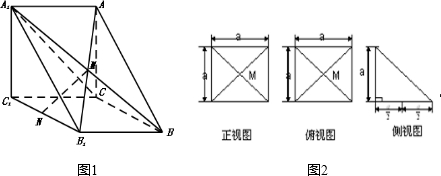 如图1,三棱柱是ABC-A1B1C1直三棱柱,它的三视图如图2所示(N为B1C1中点).
如图1,三棱柱是ABC-A1B1C1直三棱柱,它的三视图如图2所示(N为B1C1中点).
(Ⅰ)求证:MN∥平面ACC1A1;
(Ⅱ)求证:MN⊥平面A1BC;
(Ⅲ)求三棱锥B-A1NC的体积.
(Ⅰ)证明:由三视图可知,三棱柱的底面为边长为a的等腰直角三角形,侧面ACC1A1,底面BCC1B1是边长为a的正方形,且面ACC1A1⊥底面BCC1B1
设A1B1中点Q,连接MN,MQ,NQ
由题意可得NQ∥A1C1,MQ∥CC1
∴NQ∥平面ACC1A1;MQ∥平面ACC1A1
∵MQ∩NQ=Q,
∴平面MNQ∥平面ACC1A1;
(Ⅱ)取AC的中点G,连接MG,NG,则MG∥BC
∵BC⊥面ACC1A1,
∴MG⊥ACC1A1,MG⊥A1C
∵NC=NA1
∴NG⊥A1C,且NG∩MG=G
∴A1C⊥平面MNG
∴MN⊥A1C
连接NB,NA1,则可得NB=NA1= =
=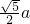
∵M为A1B的中点
∴MN⊥A1B
∵A1C∩A1B=A1
∴MN⊥平面A1BC;
(Ⅲ)解:∵S△BNC=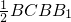 =
=
∵平面ACC1A1⊥平面BCC1B1,A1C1⊥CC1
∴A1C1⊥平面BCC1B1
∴A1C1即是点A1到平面BNC的距离
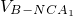 =
=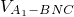 =
= =
=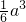
分析:(I)先由三视图可知,三棱柱的底面为边长为a的等腰直角三角形,侧面ACC1A1,底面BCC1B1是边长为a的正方形,且面ACC1A1⊥底面BCC1B1,取A1B1中点Q,可先NQ∥A1C1,MQ∥CC1即可证
(Ⅱ)取AC的中点G,可分别证明MN⊥A1B,MN⊥平面A1C,即可
(Ⅲ)由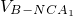 =
=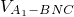 可求
可求
点评:本题是中档题,考查空间几何体的体积,直线与平面的平行,平面与平面的垂直,考查基本定理的应用,考查计算能力,空间想象能力.
设A1B1中点Q,连接MN,MQ,NQ
由题意可得NQ∥A1C1,MQ∥CC1
∴NQ∥平面ACC1A1;MQ∥平面ACC1A1
∵MQ∩NQ=Q,
∴平面MNQ∥平面ACC1A1;
(Ⅱ)取AC的中点G,连接MG,NG,则MG∥BC
∵BC⊥面ACC1A1,
∴MG⊥ACC1A1,MG⊥A1C
∵NC=NA1
∴NG⊥A1C,且NG∩MG=G
∴A1C⊥平面MNG
∴MN⊥A1C
连接NB,NA1,则可得NB=NA1=
 =
=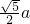
∵M为A1B的中点
∴MN⊥A1B
∵A1C∩A1B=A1
∴MN⊥平面A1BC;
(Ⅲ)解:∵S△BNC=
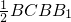 =
=
∵平面ACC1A1⊥平面BCC1B1,A1C1⊥CC1
∴A1C1⊥平面BCC1B1
∴A1C1即是点A1到平面BNC的距离
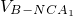 =
=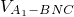 =
= =
=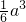
分析:(I)先由三视图可知,三棱柱的底面为边长为a的等腰直角三角形,侧面ACC1A1,底面BCC1B1是边长为a的正方形,且面ACC1A1⊥底面BCC1B1,取A1B1中点Q,可先NQ∥A1C1,MQ∥CC1即可证
(Ⅱ)取AC的中点G,可分别证明MN⊥A1B,MN⊥平面A1C,即可
(Ⅲ)由
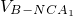 =
=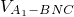 可求
可求点评:本题是中档题,考查空间几何体的体积,直线与平面的平行,平面与平面的垂直,考查基本定理的应用,考查计算能力,空间想象能力.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 如图,直三棱柱的一个底面ABC内接于圆O,AB是圆O的直径.
如图,直三棱柱的一个底面ABC内接于圆O,AB是圆O的直径.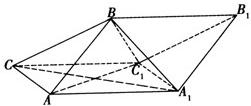 如图,斜三棱柱ABC-A1B1C1的侧面AA1C1C是面积为
如图,斜三棱柱ABC-A1B1C1的侧面AA1C1C是面积为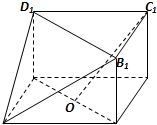 如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体中,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=2,AD=4,BB1=1.
如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体中,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=2,AD=4,BB1=1. (2012•奉贤区二模)如图,直三棱柱ABC-A1B1C1中,AA1=AB=AC=1,AB⊥AC,M是CC1的中点,N是BC的中点,点P在直线A1B1上,且满足
(2012•奉贤区二模)如图,直三棱柱ABC-A1B1C1中,AA1=AB=AC=1,AB⊥AC,M是CC1的中点,N是BC的中点,点P在直线A1B1上,且满足 如图,直三棱柱ABC-A1B1C1中,AB=
如图,直三棱柱ABC-A1B1C1中,AB=