题目内容
设m,n,k∈N*,且m≤n,k≤n,n≥2,给出下列四个命题:
①
=
; ②在(1+x)n的展开式中,若只有x4的系数最大,则n=7;
③k
=n
; ④
+2
+3
+…+n
=n•2n-1.
其中正确命题的个数有( )
①
| C | m n |
| C | n-m n |
③k
| C | k n |
| C | k-1 n-1 |
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
其中正确命题的个数有( )
分析:利用二项式系数的性质可得①正确,②不正确,由组合数的计算公式可得③正确,根据kCkn=nCk-1n-1 ,可得④正确,从而得出结论.
解答:解:由于m,n,k∈N*,且m≤n,k≤n,n≥2,利用二项式系数的性质可得①
=
成立,故①正确.
②在(1+x)n的展开式中,若只有x4的系数最大,故只有
最大,故n=8,故②不正确.
再由组合数的计算公式可得k
=
=
,n
=
=
,
故③正确.
④根据
+2
+3
+…+n
=nCn-10+nCn-11+nCn-12+nCn-13+…+nCn-1n-1
=n(Cn-10+Cn-11+Cn-12+Cn-13++Cn-1n-1)=n•2n-1,故④正确.
综上,①③④正确,②不正确,
故选C.
| C | m n |
| C | n-m n |
②在(1+x)n的展开式中,若只有x4的系数最大,故只有
| C | 4 n |
再由组合数的计算公式可得k
| C | k n |
| k•n! |
| k!(n-k)! |
| n! |
| (k-1)!(n-k)! |
| C | k-1 n-1 |
| n•(n-1)! |
| (k-1)!•(n-k)! |
| n! |
| (k-1)!(n-k)! |
故③正确.
④根据
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
=n(Cn-10+Cn-11+Cn-12+Cn-13++Cn-1n-1)=n•2n-1,故④正确.
综上,①③④正确,②不正确,
故选C.
点评:本题考查组合数的计算公式和组合数的性质:
=
以及kCkn=nCk-1n-1 ,属于中档题.
| C | m n |
| C | n-m n |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
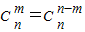 ; ②在(1+x)n的展开式中,若只有x4的系数最大,则n=7;
; ②在(1+x)n的展开式中,若只有x4的系数最大,则n=7; ; ④
; ④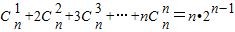 .
.