题目内容
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
(1)试分别估计元件A、元件B为正品的概率;
(2)生产一件元件A,若是正品可盈利50元,若是次品则亏损10元;生产一件元件B,若是正品可盈利100元,若是次品则亏损20元,在(1)的前提下;
(i)求生产5件元件B所获得的利润不少于300元的概率;
(ii)记X为生产1件元件A和1件元件B所得的总利润,求随机变量X的分布列和数学期望.
| 测试指标 |  |  |  |  | 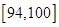 |
| 元件A | 8 | 12 | 40 | 32] | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
(2)生产一件元件A,若是正品可盈利50元,若是次品则亏损10元;生产一件元件B,若是正品可盈利100元,若是次品则亏损20元,在(1)的前提下;
(i)求生产5件元件B所获得的利润不少于300元的概率;
(ii)记X为生产1件元件A和1件元件B所得的总利润,求随机变量X的分布列和数学期望.
(1)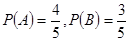 ;(2)
;(2)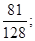 详见解析.
详见解析.
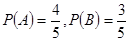 ;(2)
;(2)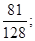 详见解析.
详见解析.试题分析:(1)由题设条件能求出元件
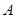 为正品的概率和元件
为正品的概率和元件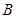 为正品的概率.
为正品的概率.(2)(i)设生产的5件元件中正品件数为
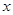 ,则有次品
,则有次品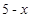 件,由题意知
件,由题意知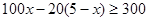 ,由此能求出生产5件元件B所获得的利润不少于300元的概率.
,由此能求出生产5件元件B所获得的利润不少于300元的概率.(ii)随机变量
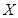 的所有取值为
的所有取值为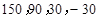 ,分别求出
,分别求出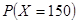 ,
,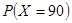 ,
,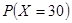 ,
,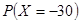 ,由此能求出
,由此能求出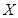 的分布列和
的分布列和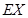 .
.试题解析:(1)由题可知元件A为正品的概率为
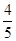 ,元件B为正品的概率为
,元件B为正品的概率为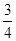 。 2分
。 2分(2)(i)设生产的5件元件中正品件数为
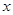 ,则有次品5
,则有次品5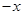 件,由题意知
件,由题意知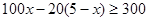 得到
得到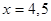 ,设“生产5件元件B所获得的利润不少于300元”为事件
,设“生产5件元件B所获得的利润不少于300元”为事件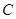 ,则
,则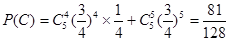 。 6分
。 6分(ii)随机变量
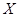 的所有取值为150,90,30,-30,
的所有取值为150,90,30,-30,则
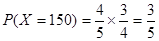 ,
,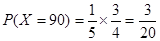 ,
,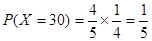 ,
,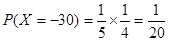 ,所以
,所以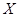 的分布列为:
的分布列为: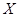 | 150 | 90 | 30 | -30 |
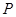 | 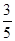 | 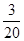 | 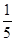 | 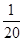 |
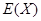
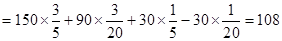 12分
12分
练习册系列答案
相关题目

 的值;
的值; (单位支),当n≥X时,求利润Y的表达式;
(单位支),当n≥X时,求利润Y的表达式; 名志愿者利用周末和节假日参加社会公益活动,活动内容是:1、到各社区宣传慰问,倡导文明新风;2、到指定的医院、福利院做义工,帮助那些需要帮助的人.各位志愿者根据各自的实际情况,选择了不同的活动项目,相关的数据如下表所示:
名志愿者利用周末和节假日参加社会公益活动,活动内容是:1、到各社区宣传慰问,倡导文明新风;2、到指定的医院、福利院做义工,帮助那些需要帮助的人.各位志愿者根据各自的实际情况,选择了不同的活动项目,相关的数据如下表所示:
 ,
,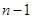 ,
,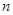 这
这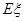 ,则
,则 ________.
________. ,
, ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为 是一个随机变量,其分布列为
是一个随机变量,其分布列为 ,则
,则 的值为( )
的值为( )



 ,乙每次击中目标的概率为
,乙每次击中目标的概率为 .
.


