Question

（选修4-1：几何证明选讲）从⊙O外一点P向圆引两条切线PA、PB和割线PCD．从点A作弦AE平行于CD，连接BE交CD于F．求证：BE平分CD．

Answer 1

分析：由弦AE平行于CD，可得∠PFB=∠AEB，根据切线长定理可得∠POB=∠AEB，进而可得O，F，B，P四点共圆，再由圆周角定理可得∠OFP=90°，再由垂径定理可得CF=DF

解答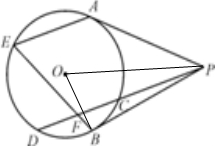： 证明：∵AE∥CD
∴∠PFB=∠AEB
又PA，PB均⊙O的切线
故OP平分

AB

，由圆周角定理和圆心圆定理可得∠POB=∠AEB
∴∠PFB=∠POB
由四点共圆判定定理的推论可得O，F，B，P四点共圆
又由PB为圆O的切线，OB为过切点的半径
可得∠OBP=90°
再由同弧或等弧所对的圆周角相等可得∠OFP=90°
再由垂径定理可得CF=DF

点评：本题考查的知识点是圆内接四边形，圆周角定理，垂径定理，其中判断出O，F，B，P四点共圆是解答的关键，本题用到的知识点比较多，相互转化也比较困难，难度较大．