题目内容
在△ABC中，点D、E分别在边AB、AC上且DE∥BC，| S△ADE |
| S△ABC |
| 4 |
| 9 |
| AE |
| EC |
| S△ADE |
| S△CDE |
分析：根据两条直线平行得到两个三角形相似，相似三角形的面积之比等于三角形的对应边之比，得到对应边之比，求出所要的结果，根据两个三角形是同高的三角形，得到三角形的面积之比等于底边之比．
解答：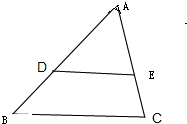
解：∵DE∥BC，
∴△ADE∽△ABC，
∴
=
=
∴
=
∴
=2
过D做AC的垂线，垂线长记做h，
∴
=
=
=2
故答案为：2；2
解：∵DE∥BC，∴△ADE∽△ABC，
∴
| S△ADE |
| S△ABC |
| 4 |
| 9 |
| AE2 |
| AC2 |
∴
| AE |
| AC |
| 2 |
| 3 |
∴
| AE |
| EC |
过D做AC的垂线，垂线长记做h，
∴
| S△ADE |
| S△CDE |
| ||
|
| AE |
| EC |
故答案为：2；2
点评：本题考查平行线分线段成比例，本题解题的关键是相似三角形的性质，利用性质求出有关的比值，本题是一个基础题．
练习册系列答案
相关题目
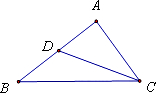如图所示，在△ABC中，点D是边AB的中点，则向量| DC |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|