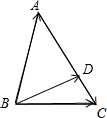
题目内容
在△ABC中,点D满足| AD |
| DC |
| BD |
| BA |
| CB |
分析:由于点D满足
=3
,可得
=
,又
=
-
,可得
=
+
=
-
.与
=λ
-μ
比较即可得出.
| AD |
| DC |
| AD |
| 3 |
| 4 |
| AC |
| AC |
| BC |
| BA |
| BD |
| BA |
| AD |
| 1 |
| 4 |
| BA |
| 3 |
| 4 |
| CB |
| BD |
| BA |
| CB |
解答:解:∵点D满足
=3
,
∴
=
,
又
=
-
,
∴
=
(
-
),
∴
=
+
=
+
(
-
)=
-
.
又
=λ
-μ
,
∴λ=
,μ=
.
∴λμ=
×
=
.
故答案为:
.
| AD |
| DC |

∴
| AD |
| 3 |
| 4 |
| AC |
又
| AC |
| BC |
| BA |
∴
| AD |
| 3 |
| 4 |
| BC |
| BA |
∴
| BD |
| BA |
| AD |
| BA |
| 3 |
| 4 |
| BC |
| BA |
| 1 |
| 4 |
| BA |
| 3 |
| 4 |
| CB |
又
| BD |
| BA |
| CB |
∴λ=
| 1 |
| 4 |
| 3 |
| 4 |
∴λμ=
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 16 |
故答案为:
| 3 |
| 16 |
点评:本题考查了向量的共线定理及其运算法则、平面向量的基本定理,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在△ABC中, 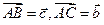 ,若点D满足
,若点D满足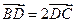 ,则
,则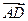 等于( )
等于( )
A.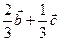 | B.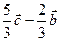 | C.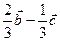 | D.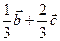 |
 ,若点D满足
,若点D满足 ,则
,则 等于( )
等于( ) B.
B.
 C.
C.
 D.
D.

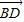 =2
=2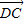 ,用
,用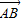 和
和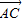 表示
表示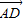 .
.