题目内容
在等差数列![]() 中,公差
中,公差![]() 的等差中项.已知数列
的等差中项.已知数列![]() 成等比数列,求数列
成等比数列,求数列![]() 的通项
的通项![]()
解:依题设得:an=a1+(n-1)d,![]()
∴![]() ,整理得d2=a1d,
,整理得d2=a1d,
∵d≠0∴d=a1,得an=nd.
所以,由已知得d,3d,k1d,k2d,…,knd,…是等比数列.
由d≠0,所以数列1,3,k1,k2,…,kn,…
也是等比数列,首项为1,公比为q=![]() =3,由此得k1=9.
=3,由此得k1=9.
等比数列{kn}的首项k1=9,公比q=3,所以kn=9×qn-2=3n+1(n=1,2,3,…).即得到数列{kn}的通项为kn=3n+1.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
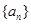 中,公差
中,公差 ,前
,前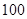 项的和
项的和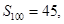
 __________________.
__________________.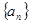 中,公差
中,公差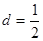 ,前
,前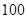 项的和
项的和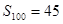 ,则
,则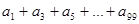 =______
=______