题目内容
已知 .
.
(1)若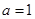 ,求曲线
,求曲线 在点
在点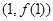 处的切线方程;
处的切线方程;
(2)若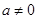 求函数
求函数 的单调区间.
的单调区间.
(1)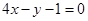 ;(2)当
;(2)当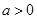 时,
时, 的单调递减区间为
的单调递减区间为 ,单调递增区间为
,单调递增区间为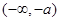 ,
,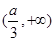 ;当
;当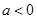 时,
时, 的单调递减区间为
的单调递减区间为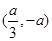 ,单调递增区间为
,单调递增区间为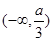 ,
,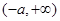 .
.
解析试题分析:(1)当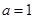 时,先求出
时,先求出 ,根据导数的几何意义可得切线的斜率
,根据导数的几何意义可得切线的斜率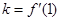 ,进而计算出
,进而计算出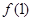 确定切点坐标,最后由点斜式即可写出切线的方程并化成直线方程的一般式;(2)先求导并进行因式分解
确定切点坐标,最后由点斜式即可写出切线的方程并化成直线方程的一般式;(2)先求导并进行因式分解 ,求出
,求出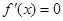 的两个解
的两个解 或
或 ,针对两根的大小进行分类讨论即分
,针对两根的大小进行分类讨论即分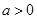 、
、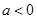 两类进行讨论,结合二次函数的图像与性质得出函数
两类进行讨论,结合二次函数的图像与性质得出函数 的单调区间,最后再将所讨论的结果进行阐述,问题即可解决.
的单调区间,最后再将所讨论的结果进行阐述,问题即可解决.
试题解析:(1) ∵ 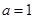 ∴
∴ ∴
∴  2分
2分
∴ 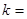
 , 又
, 又 ,所以切点坐标为
,所以切点坐标为
∴ 所求切线方程为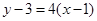 ,即
,即 5分
5分
(2)
由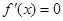 得
得 或
或 7分
7分
①当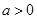 时,由
时,由 , 得
, 得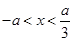 ,由
,由 , 得
, 得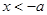 或
或 9分
9分
此时 的单调递减区间为
的单调递减区间为 ,单调递增区间为
,单调递增区间为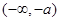 和
和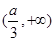 10分
10分
②当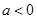 时,由
时,由 ,得
,得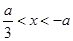 ,由
,由 ,得
,得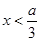 或
或 12分
12分
此时 的单调递减区间为
的单调递减区间为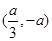 ,单调递增区间为
,单调递增区间为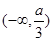 和
和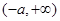 13分
13分
综上:当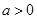 时,
时, 的单调递减区间为
的单调递减区间为 ,单调递增区间为
,单调递增区间为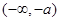 ,
,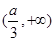 ;当
;当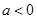 时,
时, 的单调递减区间为
的单调递减区间为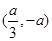 单调递增区间为
单调递增区间为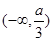 ,
,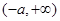 14分.
14分.
考点:1.导数的几何意义;2.函数的单调性与导数;3.分类讨论的思想.

练习册系列答案
相关题目
 ,其中b≠0.
,其中b≠0. 时,判断函数
时,判断函数 在定义域上的单调性:
在定义域上的单调性: ,其中m,a均为实数.
,其中m,a均为实数. 的极值;
的极值; ,若对任意的
,若对任意的
 ,
, 恒成立,求
恒成立,求 的最小值;
的最小值; ,若对任意给定的
,若对任意给定的 ,在区间
,在区间 上总存在
上总存在 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围. ,其中
,其中 .
.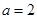 时,求函数
时,求函数 的图象在点
的图象在点 处的切线方程;
处的切线方程;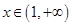 ,都有
,都有 ,求
,求 的取值范围.
的取值范围. .
.
 时,求
时,求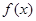 的极值;
的极值; 时,讨论
时,讨论 ,恒有
,恒有 成立,求实数
成立,求实数 的取值范围.
的取值范围. 在
在 处有极大值
处有极大值 .
. 的解析式;
的解析式;