题目内容
过点P(1,4)引一条直线l,使它在两条坐标轴上的截距都是正数且它们的和最小,求直线l的方程.
【答案】分析:设直线方程为 (a>0,b>0),得
(a>0,b>0),得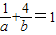 ,进而得到l在两条坐标轴上的截距的和a+b=(a+b)(
,进而得到l在两条坐标轴上的截距的和a+b=(a+b)( )=5+
)=5+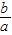 +
+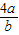 ,最后利用基本不等式求最值,根据取等号的条件得出a、b之值,即可得出直线l的方程.
,最后利用基本不等式求最值,根据取等号的条件得出a、b之值,即可得出直线l的方程.
解答:解:设直线方程为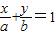 (a>0,b>0)
(a>0,b>0)
∵P(1,4)在直线l上,
∴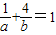 ,
,
由此可得直线l在两条坐标轴上的截距的和满足
a+b=(a+b)(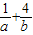 )=5+
)=5+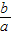 +
+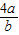
∵a>0,b>0,得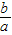 +
+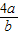 ≥2
≥2 =4
=4
∴当且仅当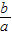 =
=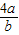 =2时,即a=3且b=6时,
=2时,即a=3且b=6时,
直线l在两条坐标轴上的截距的和得最小值为5+4=9
此时直线方程为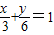 ,即2x+y-6=0
,即2x+y-6=0
∴直线l的方程是2x+y-6=0.
点评:本题给出经过点P(1,4)且与两坐标轴交于正半轴的直线l,求l在两轴截距和最小时直线l的方程,着重考查了直线的基本量与基本形式和基本不等式等知识,属于中档题.
 (a>0,b>0),得
(a>0,b>0),得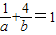 ,进而得到l在两条坐标轴上的截距的和a+b=(a+b)(
,进而得到l在两条坐标轴上的截距的和a+b=(a+b)( )=5+
)=5+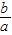 +
+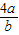 ,最后利用基本不等式求最值,根据取等号的条件得出a、b之值,即可得出直线l的方程.
,最后利用基本不等式求最值,根据取等号的条件得出a、b之值,即可得出直线l的方程.解答:解:设直线方程为
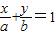 (a>0,b>0)
(a>0,b>0)∵P(1,4)在直线l上,
∴
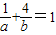 ,
,由此可得直线l在两条坐标轴上的截距的和满足
a+b=(a+b)(
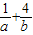 )=5+
)=5+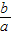 +
+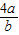
∵a>0,b>0,得
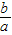 +
+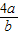 ≥2
≥2 =4
=4∴当且仅当
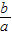 =
=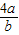 =2时,即a=3且b=6时,
=2时,即a=3且b=6时,直线l在两条坐标轴上的截距的和得最小值为5+4=9
此时直线方程为
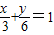 ,即2x+y-6=0
,即2x+y-6=0∴直线l的方程是2x+y-6=0.
点评:本题给出经过点P(1,4)且与两坐标轴交于正半轴的直线l,求l在两轴截距和最小时直线l的方程,着重考查了直线的基本量与基本形式和基本不等式等知识,属于中档题.

练习册系列答案
相关题目