题目内容
若a,b是正常数,a≠b,x,y∈(0,+∞),则 +
+ ≥
≥ ,当且仅当
,当且仅当 =
= 时取等号.利用以上结论,函数f(x)=
时取等号.利用以上结论,函数f(x)= +
+ (x∈(0,
(x∈(0, ))取得最小值时x的值为( )
))取得最小值时x的值为( )A.1
B.

C.2
D.

【答案】分析:由“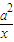 +
+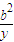 ≥
≥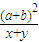 ”可得f(x)=
”可得f(x)=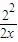 +
+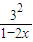 ≥
≥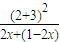 ,再由取得等号的条件,求最小值.
,再由取得等号的条件,求最小值.
解答:解析:由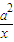 +
+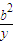 ≥
≥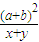
得:f(x)=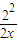 +
+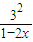 ≥
≥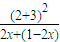 =25.
=25.
当且仅当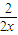 =
=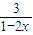 时取等号,
时取等号,
即当x=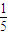 时f(x)取得最小值25.
时f(x)取得最小值25.
故选B.
点评:本题主要考查用基本不等式求函数最值问题,关键是基本不等式的应用条件:一正,二定,三相等.
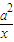 +
+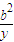 ≥
≥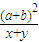 ”可得f(x)=
”可得f(x)=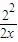 +
+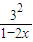 ≥
≥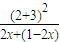 ,再由取得等号的条件,求最小值.
,再由取得等号的条件,求最小值.解答:解析:由
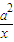 +
+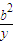 ≥
≥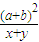
得:f(x)=
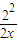 +
+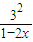 ≥
≥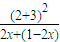 =25.
=25.当且仅当
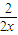 =
=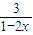 时取等号,
时取等号,即当x=
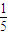 时f(x)取得最小值25.
时f(x)取得最小值25.故选B.
点评:本题主要考查用基本不等式求函数最值问题,关键是基本不等式的应用条件:一正,二定,三相等.

练习册系列答案
相关题目
 (2012•湖南模拟)选做题(请考生在第16题的三个小题中任选两题作答,如果全做,则按前两题记分,要写出必要的推理与演算过程)
(2012•湖南模拟)选做题(请考生在第16题的三个小题中任选两题作答,如果全做,则按前两题记分,要写出必要的推理与演算过程)